Общая характеристика законов распределения системы случайных величин

Геогэкологические процессы определяются совокупным воздействием множества различных факторов (см. гл. 2). При их математическом анализе совокупность различных факторов часто рассматривается как система случайных величин [ ].

Система m случайных величин (X_1, Х₂, ... , Х_т) геометрически интерпретируется как координаты случайной точки в m -мерном пространстве. Иногда в этих целях используют образ случайного вектора, составляющие которого по осям представляют собой случайные величины X₁, X₂, ..., Х_т.

Функция распределения m-мерного случайного вектора или, иначе, совместная функция распределения определяется как веро­ятность совместного выполнения т неравенств

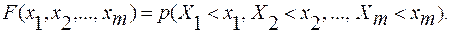
(3.56)

Свойства совместной функции распределения аналогичны свой­ствам функции распределения одной случайной величины (см. разд. 3.1.3). Кроме того, так как события X_j < -∞ (j = 1, 2, . . ., т) невозможны, то при стремлении хотя бы одного аргумента к -∞, совместная функция распределения стремится к нулю. Важно также отметить, что при стремлении какого-то j-го аргу­мента к ∞, событие становится достоверным и совместная функ­ция распределения уже не зависит от j-го аргумента. Отсюда для получения функции распределения одной или нескольких из имею­щихся случайных величин нужно все остальные аргументы поло­жить равными бесконечности.

Плотность распределения системы случайных величин или совместная плотность распределения ­– смешанная частная производная, если она существует, от совместной функции распределения, взятая 1 раз по каждому аргументу

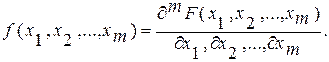
(3.57)

Свойства совместной плотности распределения во многом аналогичны свойствам плотности распределения одной случайной ве­личины (см. разд. 3.1.3). Зная плотность распределения, можно определить совместную функцию распределения

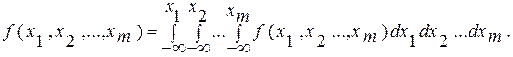(3.58)

Зная совместную плотность распределения, можно определить вероятность попадания случайной точки (X₁, X₂, …, Х_т) в пре­делы m-мерной области D по формуле

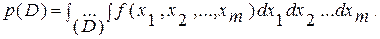
(3.59)