Метод вариации произвольных постоянных.
Этот метод применяется для отыскания частного решения линейного неоднородного дифференциального уравнения 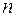 -го порядка как с переменными, так и с постоянными коэффициентами, если известно общее решение соответствующего однородного уравнения.
-го порядка как с переменными, так и с постоянными коэффициентами, если известно общее решение соответствующего однородного уравнения.
Для неоднородного линейного дифференциального уравнения 2-го порядка с постоянными коэффициентами 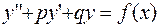 общее решение однородного уравнения имеет вид:
общее решение однородного уравнения имеет вид: 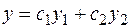 , где
, где 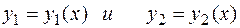 - частные решения однородного ДУ.
- частные решения однородного ДУ.
Общее решение неоднородного дифференциального уравнения находят в виде: 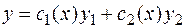 , (3.26.)
, (3.26.)
 То есть предполагается, что постоянные
То есть предполагается, что постоянные 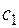 и
и 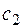 являются функциями независимой переменной
являются функциями независимой переменной 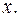 При этом функции
При этом функции 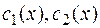 находят из системы:
находят из системы: 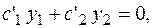
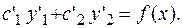 (3.27.)
(3.27.)
ПРИМЕР 3.17. Найти общее решение уравнения 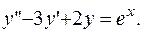
РЕШЕНИЕ. Имеем линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами.
Находим общее решение однородного уравнения. Составляем характеристическое уравнение.
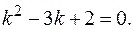 Его корни:
Его корни: 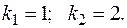
Следовательно 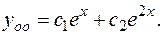
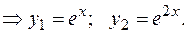
Находим общее решение неоднородного уравнения. Составляем систему согласно (3.27.).
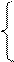
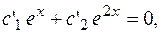 Вычитаем 1-е уравнение из 2-го и
Вычитаем 1-е уравнение из 2-го и
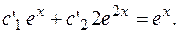 получаем:
получаем:





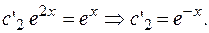
Находим 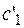 , подставив
, подставив 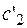 в 1-е уравнение.
в 1-е уравнение.




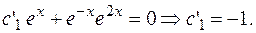
Находим 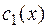 и
и 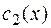 .
.
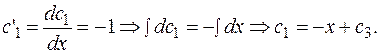

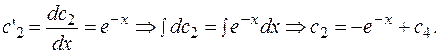
Таким образом, 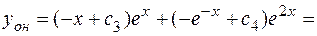
= 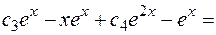
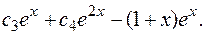
Сравнив 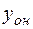 с
с 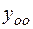 , заметим, что первые два слагаемых решения неоднородного уравнения, есть общее решение однородного уравнения. Последнее слагаемое есть частное решение исходного неоднородного уравнения:
, заметим, что первые два слагаемых решения неоднородного уравнения, есть общее решение однородного уравнения. Последнее слагаемое есть частное решение исходного неоднородного уравнения: 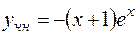 , в чем легко убедиться.
, в чем легко убедиться.
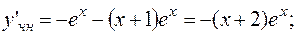
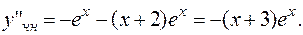
Подставляем в исходное дифференциальное уравнение:
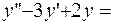
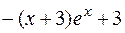
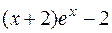
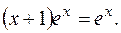
ПРИМЕР 3.18. Найти общее решение уравнения 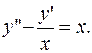
РЕШЕНИЕ. Имеем линейное неоднородное дифференциальное уравнение второго порядка с коэффициентом – функцией 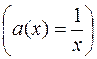 .
.
Находим общее решение однородного уравнения.
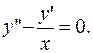 - Дифференциальное уравнение второго порядка не содержит
- Дифференциальное уравнение второго порядка не содержит 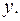 Применяем замену:
Применяем замену: 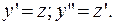 Получаем:
Получаем:
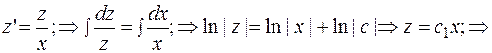
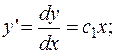
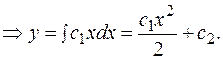
Следовательно 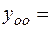
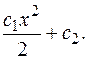
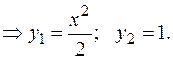
Находим коэффициенты 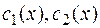 . Составляем систему согласно (3.27.).
. Составляем систему согласно (3.27.).
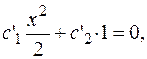
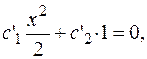
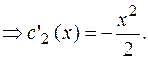

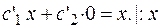
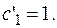
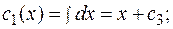
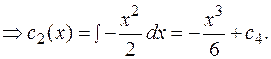
Записываем функции 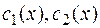 в
в 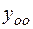 и получаем общее решение исходного неоднородного дифференциального уравнения.
и получаем общее решение исходного неоднородного дифференциального уравнения.
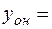
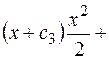
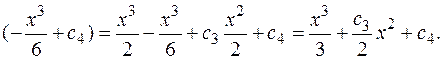
Окончательно: 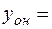
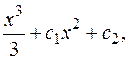 где
где 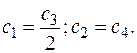
Метод вариации произвольных постоянныхдля решениялинейных дифференциальных уравнений 1-го порядка 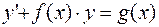
Применяют в следующем порядке:
· записывают однородное линейное уравнение 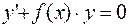 и
и
находят его решение 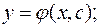
· заменяют постоянную 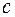 функцией
функцией 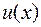 и записывают
и записывают 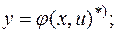
· дифференцируют обе части последнего равенства 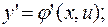
· подставляют 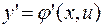 и
и 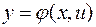 в исходное уравнение и получают:
в исходное уравнение и получают: 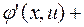
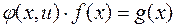 ;
;
· решают последнее уравнение и находят 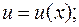
· подставляют найденную функцию 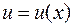 в уравнение, помеченное
в уравнение, помеченное 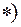 , и получаем искомое решение
, и получаем искомое решение 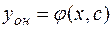 .
.
ПРИМЕР 3.19. Найти общее решение уравнения 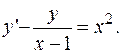
РЕШЕНИЕ. Имеем линейное неоднородное дифференциальное уравнение первого порядка.
Находим общее решение однородного уравнения. 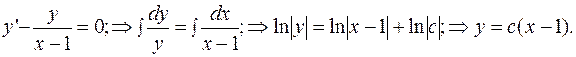
Заменяем постоянную 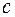 на функцию
на функцию 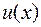 . Получаем:
. Получаем: 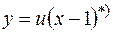 Продифференцируем обе части равенства:
Продифференцируем обе части равенства: 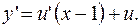
Подставляем 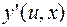 и
и 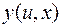 в исходное уравнение.
в исходное уравнение. 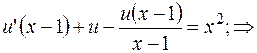
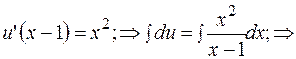

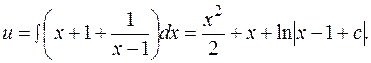
Подставляем 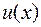 в уравнение, помеченное
в уравнение, помеченное 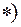 , и получаем общее решение:
, и получаем общее решение: 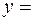
Дата добавления: 2020-10-25; просмотров: 680;











