Метод подбора частного решения по виду правой части.
Частное решение линейного неоднородного уравнения 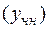 составляют для специальных видов правой части уравнения (3.13) методом неопределенных коэффициентов.
составляют для специальных видов правой части уравнения (3.13) методом неопределенных коэффициентов.
1. Правая часть имеет вид 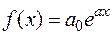 , (3.15.)
, (3.15.)
где 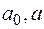 - действительные числа.
- действительные числа.
Если 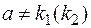 ,то
,то 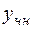 следует искать в виде
следует искать в виде 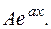 (3.16.)
(3.16.)
Если 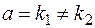 , то
, то 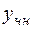 следует искать в виде
следует искать в виде 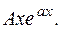 (3.17.)
(3.17.)
Если 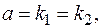 то
то 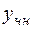 следует искать в виде
следует искать в виде 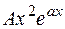 , (3.18.)
, (3.18.)
где А – неопределенный коэффициент, методика отыскания которого будет показана далее на примере.
2. Правая часть имеет вид
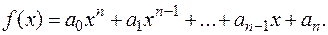 (3.19.)
(3.19.)
Если 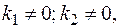 то
то 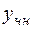 следует искать в виде
следует искать в виде
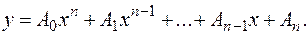 (3.20.)
(3.20.)
Если 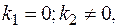 то
то 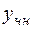 следует искать в виде
следует искать в виде
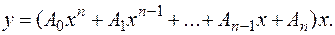 (3.21.)
(3.21.)
Если 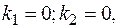 то
то 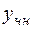 следует искать в виде
следует искать в виде
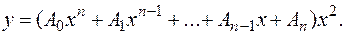 (3.22.)
(3.22.)
3. Правая часть имеет вид 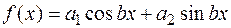 . (3.23.)
. (3.23.)
Если 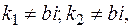 то
то 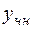 следует искать в виде
следует искать в виде
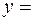
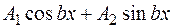 . (3.24.)
. (3.24.)
Если 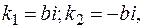 то
то 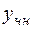 следует искать в виде
следует искать в виде
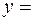
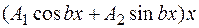 . (3.25.)
. (3.25.)
ПРИМЕР 3.11. Найти общее решение уравнения 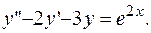
РЕШЕНИЕ. Имеем линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его решение
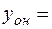
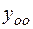 +
+ 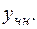
Находим общее решение однородного уравнения 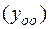 .Составляем характеристическое уравнение
.Составляем характеристическое уравнение 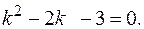
Его корни: 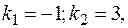 следовательно
следовательно 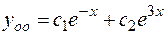 .
.
 Составляем частное решение линейного неоднородного уравнения.
Составляем частное решение линейного неоднородного уравнения. 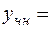
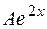 . Его и его производные надо подставить в исходное ДУ и найти коэффициент
. Его и его производные надо подставить в исходное ДУ и найти коэффициент 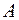 . Для этого удобно делать записи в следующем виде: -3
. Для этого удобно делать записи в следующем виде: -3 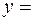
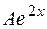
-2 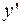 =2
=2 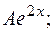
1 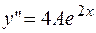 .
.

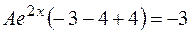
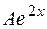
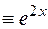 .
.
Сравнив коэффициенты при 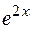 , находим:
, находим: 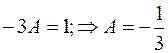 .
.
Следовательно: 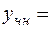
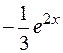 .
.
Записываем общее решение линейного неоднородного дифференциального уравнения: 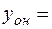
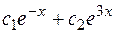
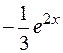 .
.
ПРИМЕР 3.12. Найти общее решение уравнения 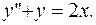
РЕШЕНИЕ. Имеем линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его решение
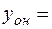
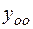 +
+ 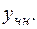
Находим общее решение однородного уравнения 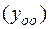 .
.
Составляем характеристическое уравнение 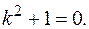
Его корни: 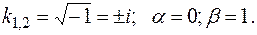
Следовательно 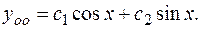
Составляем частное решение линейного неоднородного уравнения. 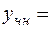
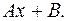 (Здесь и в дальнейшем вместо
(Здесь и в дальнейшем вместо 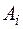 будем записывать другие буквы, чтобы не запутаться в индексах.)
будем записывать другие буквы, чтобы не запутаться в индексах.)
 1
1 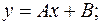
0 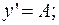
 1
1 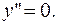
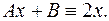
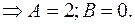
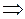
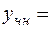
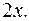
Искомое решение: 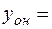
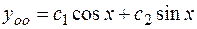 +
+ 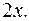
ПРИМЕР 3.13. Найти общее решение уравнения 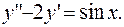
РЕШЕНИЕ. Имеем линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его решение
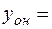
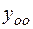 +
+ 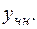
Находим общее решение однородного уравнения 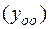 .
.
Составляем характеристическое уравнение 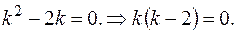 Его корни:
Его корни: 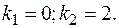
Следовательно 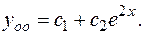
 Составляем частное решение линейного неоднородного уравнения. 0 0
Составляем частное решение линейного неоднородного уравнения. 0 0 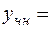
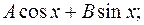
-2 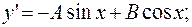
1 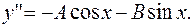

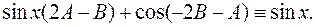
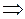 +
+ 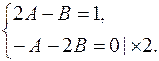

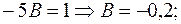
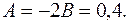 Получили:
Получили: 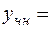
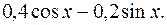
Таким образом, 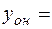
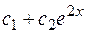
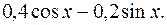
ПРИМЕР 3.14. Найти общее решение уравнения 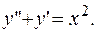
РЕШЕНИЕ. Имеем линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его решение
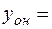
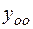 +
+ 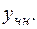
Находим общее решение однородного уравнения 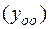 .
.
Составляем характеристическое уравнение 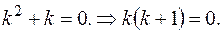 Его корни:
Его корни: 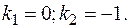
Следовательно 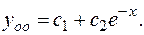
 Составляем частное решение линейного неоднородного уравнения, учитывая, что один корень характеристического уравнения нулевой 0
Составляем частное решение линейного неоднородного уравнения, учитывая, что один корень характеристического уравнения нулевой 0 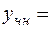
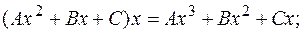
1 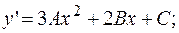
1 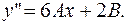

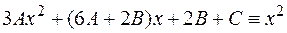
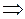
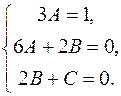
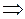
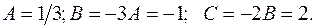
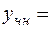
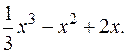
Таким образом, 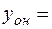
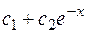 +
+ 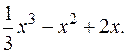
ПРИМЕР 3.15. Найти общее решение уравнения 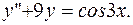
РЕШЕНИЕ. Имеем линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его решение
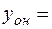
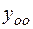 +
+ 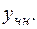
Находим общее решение однородного уравнения 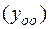 .
.
Составляем характеристическое уравнение 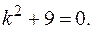 Его корни:
Его корни: 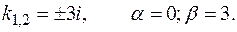
Следовательно 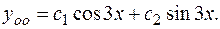
Составляем частное решение линейного неоднородного уравнения, учитывая, что 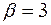 и аргумент косинуса в правой части уравнения также равен 3, то есть согласно (3.25.)
и аргумент косинуса в правой части уравнения также равен 3, то есть согласно (3.25.)
 9
9 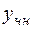 =
= 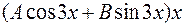 ;
;
0 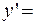
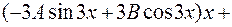
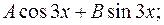
 1
1 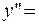
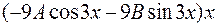
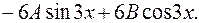
9 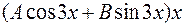
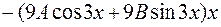
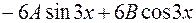 =
= 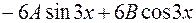
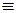
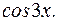
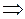
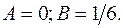
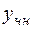 =
= 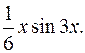
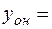
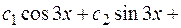
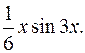
ПРИМЕР 3.16. Найти частное решение уравнения 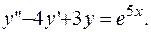
При начальных условиях: 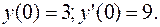
РЕШЕНИЕ. Имеем линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его решение
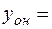
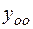 +
+ 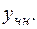
Находим общее решение однородного уравнения 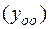 .
.
Составляем характеристическое уравнение 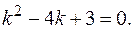 Его корни:
Его корни: 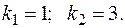
Следовательно 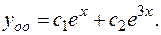
Составляем частное решение линейного неоднородного уравнения, учитывая, что среди корней характеристического уравнения нет равного 5, то есть согласно (3.16.).
 3
3 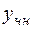 =
= 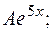
-4 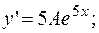
1 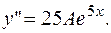
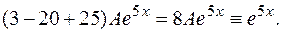
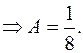
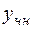 =
= 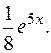
Общее решение: 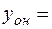
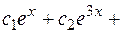
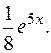
Находим частное решение по начальным условиям.
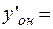
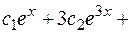
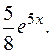
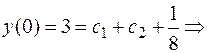
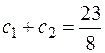
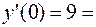
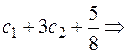
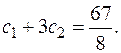
Вычтя 1-е уравнение из 2-го, получаем: 2 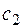 =
= 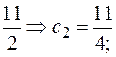
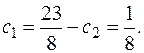 Следовательно, частное решение по начальным условиям:
Следовательно, частное решение по начальным условиям: 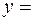
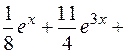
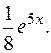
Дата добавления: 2020-10-25; просмотров: 1771;











