Линейные однородные дифференциальные уравнения с постоянными коэффициентами.
Это уравнения вида: 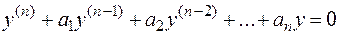 , где
, где
коэффициенты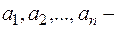 некоторыедействительные числа.
некоторыедействительные числа.
Для нахождения частных решений уравнения составляется характеристическое уравнение
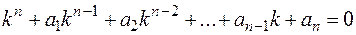 ,
,
которое получается из исходного дифференциального уравнения заменой в нём производных искомой функции соответствующими степенями параметра 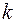 , причем сама функция заменяется единицей. Характеристическое уравнение – алгебраическое
, причем сама функция заменяется единицей. Характеристическое уравнение – алгебраическое 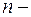 ой степени поэтому имеет
ой степени поэтому имеет 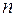 корней, действительных или комплексных, среди которых могут быть и равные.
корней, действительных или комплексных, среди которых могут быть и равные.
Общее решениелинейного однородного дифференциального уравнения с постоянными коэффициентами строится в зависимости от вида корней характеристического уравнения:
а) каждому действительному простому корню 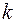 в общем решении соответствует слагаемое вида
в общем решении соответствует слагаемое вида 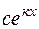 . Для дифференциального уравнения 2-го порядка это соответствует двум разным действительным корням. При этом общее решениелинейного однородного дифференциального уравнения с постоянными коэффициентами имеет вид:
. Для дифференциального уравнения 2-го порядка это соответствует двум разным действительным корням. При этом общее решениелинейного однородного дифференциального уравнения с постоянными коэффициентами имеет вид:
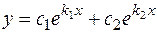 ; (3.10.)
; (3.10.)
б) каждому действительному корню кратности 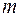 в общем решении соответствует слагаемое вида
в общем решении соответствует слагаемое вида 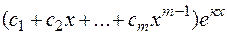 . Для дифференциального уравнения 2-го порядка это соответствует двум одинаковым действительным корням. При этом общее решениелинейного однородного дифференциального уравнения с постоянными коэффициентами имеет вид:
. Для дифференциального уравнения 2-го порядка это соответствует двум одинаковым действительным корням. При этом общее решениелинейного однородного дифференциального уравнения с постоянными коэффициентами имеет вид:
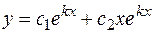 ; (3.11.)
; (3.11.)
в) каждой паре комплексных сопряженных корней 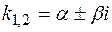 в общем решении соответствует слагаемое вида
в общем решении соответствует слагаемое вида 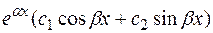 . Для дифференциального уравнения 2-го порядка это соответствует одной паре комплексных сопряженных корней. При этом общее решениелинейного однородного дифференциального уравнения с постоянными коэффициентами имеет такой же вид:
. Для дифференциального уравнения 2-го порядка это соответствует одной паре комплексных сопряженных корней. При этом общее решениелинейного однородного дифференциального уравнения с постоянными коэффициентами имеет такой же вид:
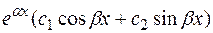 . (3.12.)
. (3.12.)
ПРИМЕР 3.7. Найти общее решение дифференциального уравнения 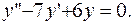
РЕШЕНИЕ. Составляем характеристическое уравнение
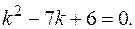
Его корни определяем по теореме Виета: 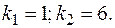
Следовательно, частные решения: 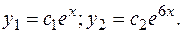
Общее решение: 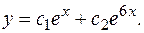

ПРИМЕР 3.8. Найти частное решение дифференциального уравнения 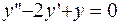 при начальных условиях:
при начальных условиях: 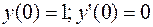 .
.
РЕШЕНИЕ. Составляем характеристическое уравнение
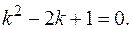 Его корни:
Его корни: 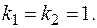
Следовательно, его частные линейно независимые решения:
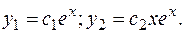
Общее решение: 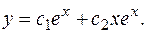

Находим частное решение по начальным условиям.

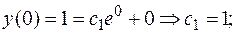

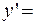
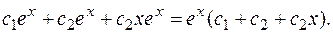
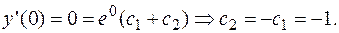
Таким образом, частное решение по начальным условиям:
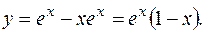
ПРИМЕР 3.9. Найти частное решение дифференциального уравнения 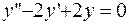 при начальных условиях:
при начальных условиях: 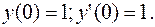
РЕШЕНИЕ. Составляем характеристическое уравнение
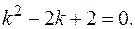 Его корни:
Его корни: 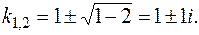
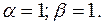
Следовательно общее решение: 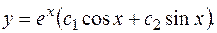
Находим частное решение по начальным условиям.
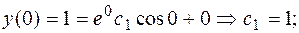
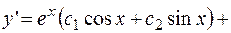
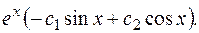
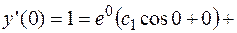
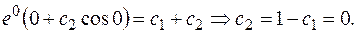
Таким образом, искомое частное решение: 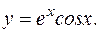
ПРИМЕР 3.10. Найти общее решение дифференциального уравнения 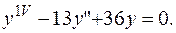
РЕШЕНИЕ. Составляем характеристическое уравнение
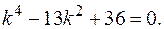 Его корни:
Его корни: 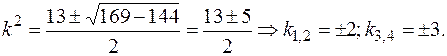
Все корни действительные разные. Им соответствуют линейно независимые частные решения: 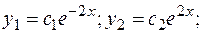
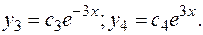
Следовательно, общее решение: 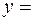
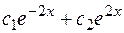
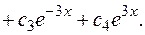
Дата добавления: 2020-10-25; просмотров: 606;











