Линейные дифференциальные уравнения высшего порядка.
Дифференциальное уравнение вида:
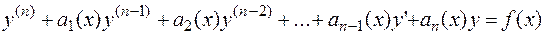
называется линейным неоднородным дифференциальным уравнением
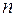 -го порядка или линейным дифференциальным уравнением с правой частью. Если правая часть уравнения равна нулю (
-го порядка или линейным дифференциальным уравнением с правой частью. Если правая часть уравнения равна нулю ( 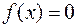 ), то - линейным однородным дифференциальным уравнением
), то - линейным однородным дифференциальным уравнением 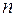 -го порядка.
-го порядка.
Линейное однородное дифференциальное уравнение с той же левой частью, что и улинейного неоднородного дифференциального уравнения того же порядка, называется соответствующим ему.
Зная одно частное решение 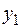 линейного однородного дифференциального уравнения, можно понизить его порядок, выполнив замену
линейного однородного дифференциального уравнения, можно понизить его порядок, выполнив замену 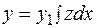 . Полученное дифференциальное уравнение
. Полученное дифференциальное уравнение 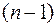 -го
-го
порядка относительно 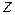 также является линейным.
также является линейным.
Общее решение линейного однородного дифференциального уравнения можно найти по известным частным решениям.
Теорема: "если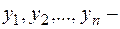 линейно независимые частные решения уравнения
линейно независимые частные решения уравнения 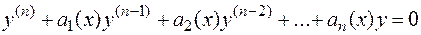 ,
,
то 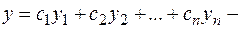 есть общее решение этого уравнения.
есть общее решение этого уравнения.
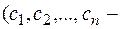 произвольные постоянные).
произвольные постоянные).
Совокупность 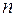 решений линейного однородного дифференциального уравнения
решений линейного однородного дифференциального уравнения 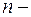 го порядка, определенных и линейно независимых в промежутке [a,b], называется фундаментальной системой решений этого уравнения.
го порядка, определенных и линейно независимых в промежутке [a,b], называется фундаментальной системой решений этого уравнения.
Для линейного однородного дифференциального уравнения 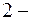 го порядка
го порядка 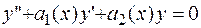 фундаментальная система решений
фундаментальная система решений
состоит из двух линейно независимых решений 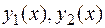 . Его общее решение находится по формуле:
. Его общее решение находится по формуле:
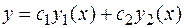 .
.  (3.9.)
(3.9.)
Дата добавления: 2020-10-25; просмотров: 549;











