Метод решения дифференциальных уравнений с помощью рядов.
Для приближенного решениядифференциального уравнения применяют ряд Тейлора или Макларена в зависимости от начального условия 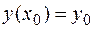 . Так, если
. Так, если 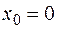 , то применяют ряд Макларена, если
, то применяют ряд Макларена, если 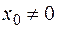 , то - ряд Тейлора.
, то - ряд Тейлора.
Решение записывают в виде бесконечного ряда
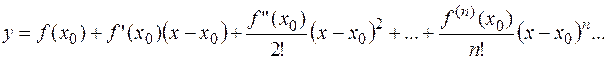 Значение
Значение 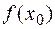 =
= 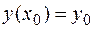 . Значение
. Значение 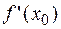 находят, подставив
находят, подставив 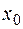 и
и 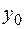 в исходное дифференциальное уравнение. Значения остальных производных в точке
в исходное дифференциальное уравнение. Значения остальных производных в точке 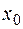 вычисляют, найдя предварительно саму производную и подставив в неё
вычисляют, найдя предварительно саму производную и подставив в неё 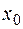 ,
, 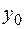 и производные более низкого порядка, вычисленные ранее.
и производные более низкого порядка, вычисленные ранее.
После вычисления коэффициентов получают решение в виде степенного ряда с постоянными коэффициентами. Далее вычисляют значения функции для заданных значений аргумента с заданной точностью.
Решение дифференциального уравнения записывают дискретно.
ПРИМЕР 4.2. Найти приближенное решение дифференциального уравнения 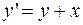 для аргумента
для аргумента 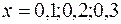 с точностью
с точностью 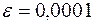 , если
, если 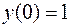 .
.
РЕШЕНИЕ. Имеем дифференциальное уравнение первого порядка.
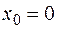 . Следовательно решение записываем в виде ряда Тейлора
. Следовательно решение записываем в виде ряда Тейлора 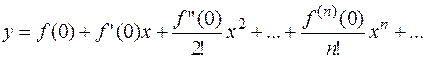
Находим коэффициенты ряда.
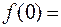
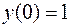 ;
; 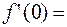
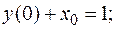
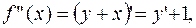
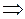
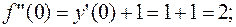
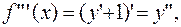
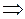
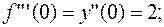
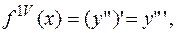
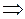
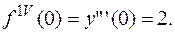
Видим, что далее коэффициенты повторяются.
Получили решение в виде бесконечного степенного ряда
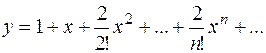
Запишем первые пять членов ряда:
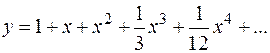
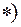
Вычисляем значения этой функции для заданных значений аргумента.
При 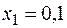 получаем
получаем 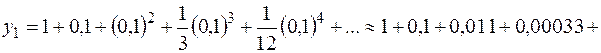
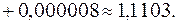 Для вычисления взяты 4 члена ряда. Убедимся, что этого достаточно, то есть сумма отброшенных членов не превышает погрешности вычисления. Для этого рассмотрим остаток
Для вычисления взяты 4 члена ряда. Убедимся, что этого достаточно, то есть сумма отброшенных членов не превышает погрешности вычисления. Для этого рассмотрим остаток 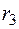 (считая первое слагаемое нулевым членом)
(считая первое слагаемое нулевым членом)
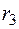 =
= 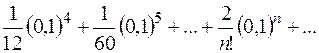

Заменяем неравенством
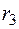 <
< 
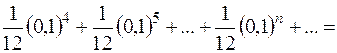
= 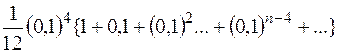
В фигурных скобках имеем бесконечную убывающую геометрическую прогрессию со знаменателем 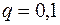 . Сумма членов такой прогрессии
. Сумма членов такой прогрессии 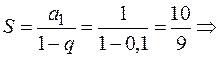
Остаток 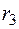 <
< 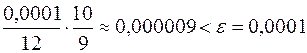 .
.
Следовательно, для вычисления значения функции достаточно взять четыре члена (считая нулевой).
При 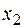
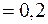 получаем
получаем 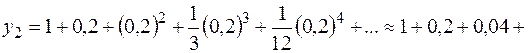
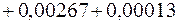 +
+ 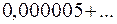
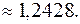
При 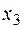
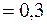 получаем
получаем
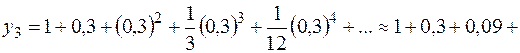
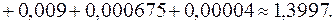
Таким образом, решение дифференциального уравнения:
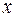
| 0,1 | 0,2 | 0,3 | … |
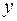
| 1,1103 | 1,2428 | 1,3997 | … |
V.ПОНЯТИЕ О СИСТЕМАХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ И МЕТОДАХ ИХ РЕШЕНИЙ.
 При решении многих задач требуется найти функции
При решении многих задач требуется найти функции 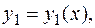
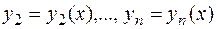 , которые удовлетворяют системе дифференциальных уравнений вида:
, которые удовлетворяют системе дифференциальных уравнений вида: 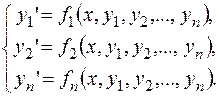 (5.1.)
(5.1.)
где искомые функции,
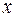 - аргумент.
- аргумент.
Система (5.1.), в которой левые части уравнений содержат производные первого порядка, а правые части производных не содержат, называется нормальной.
Система, в которой правые части нормальной системы дифференциальных уравнений являются линейными функциями относительно 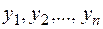 , называется линейной.
, называется линейной.
Решить (проинтегрировать) систему – значит определить функции
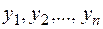 , удовлетворяющие системе (5.1.) и данным начальным условиям:
, удовлетворяющие системе (5.1.) и данным начальным условиям:
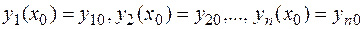 (5.2.)
(5.2.)
Иногда нормальную систему дифференциальных уравнений удается свести к одному уравнению 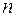 - го порядка, содержащему одну неизвестную переменную. Это достигается дифференцированием одного из уравнений системы и исключением из него всех неизвестных, кроме одного. Этот метод называется методом исключений.
- го порядка, содержащему одну неизвестную переменную. Это достигается дифференцированием одного из уравнений системы и исключением из него всех неизвестных, кроме одного. Этот метод называется методом исключений.
Система(5.1.) решается следующим образом.
1) Дифференцируют по аргументу 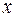 одно из уравнений системы, например, первое
одно из уравнений системы, например, первое 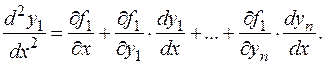
2) Заменяют в полученном дифференциальном уравнении 2-го порядка производные 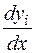 их выражениями из (5.1.) и получают:
их выражениями из (5.1.) и получают: 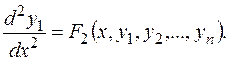 (5.3.)
(5.3.)
3) Из 1 – го уравнения системы(5.1.) выражают 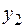 и подставляют в (5.3.). Таким образом исключается переменная
и подставляют в (5.3.). Таким образом исключается переменная 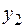 .
.
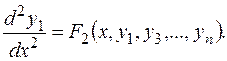
Дифференцируют это уравнение. Заменив в нем 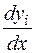 аналогично предыдущему шагу, получают дифференциальное уравнении 3-го порядка:
аналогично предыдущему шагу, получают дифференциальное уравнении 3-го порядка:
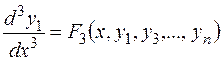 , из которого исключают
, из которого исключают 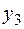 .
.
4) Продолжая дифференцировать и заменять переменные 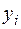 , получают дифференциальное уравнение
, получают дифференциальное уравнение 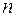 -го порядка одной переменной:
-го порядка одной переменной: 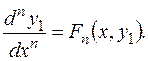 (5.4.)
(5.4.)
Решив данное уравнение, находят 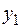 =
= 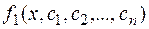
5) Последовательно находят 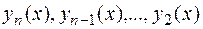 и записывают решение в виде системы
и записывают решение в виде системы

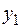 =
= 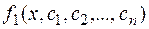 ,
,
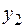 =
= 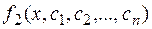 , (5.5.)
, (5.5.)

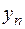 =
= 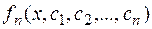 .
.
ПРИМЕР 5.1. Проинтегрировать систему 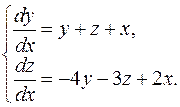
При начальных условиях: 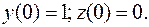
РЕШЕНИЕ.
Дифференцируя по 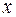 первое уравнение, получаем:
первое уравнение, получаем: 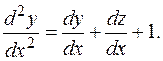
Подставляем в это уравнение функции 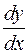 и
и 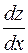 из исходной системы. Получаем:
из исходной системы. Получаем: 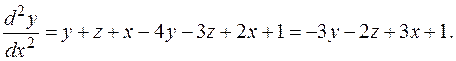
Из первого уравнения системы получаем: 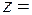
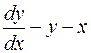 и подставляем в предыдущее уравнение:
и подставляем в предыдущее уравнение:
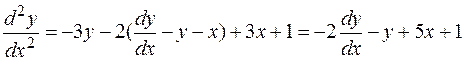
или 
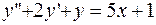 - линейное неоднородное дифференциальное уравнение 1- го порядка с постоянными коэффициентами
- линейное неоднородное дифференциальное уравнение 1- го порядка с постоянными коэффициентами 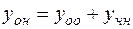 .
.
Находим общее решение однородного уравнения.
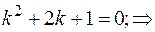
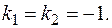
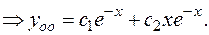
 Находим частное решение неоднородного уравнения по виду правой части. 1
Находим частное решение неоднородного уравнения по виду правой части. 1 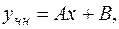
2 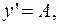
 1
1 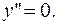
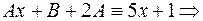
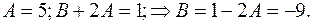
Получили 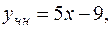
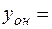
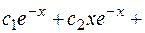
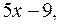
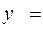
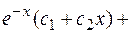
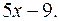
Находим вторую переменную. 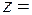
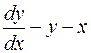 =
=
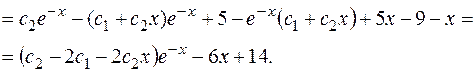
Общее решение исходной системы:

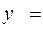
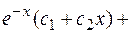
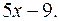
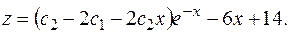
Находим частное решение по начальным условиям.

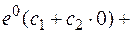
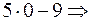
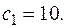
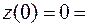
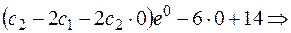
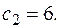
Частное решение:

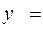
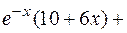
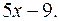
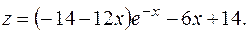
В некоторых случаях, комбинируя уравнения системы, после несложных преобразований удается получить легко интегрируемые уравнения, что позволяет найти решение системы. Этот метод называется методом интегрируемых комбинаций.
ПРИМЕР 5.2. Проинтегрировать систему 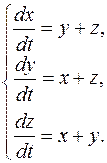
РЕШЕНИЕ.
Дифференцируя по 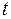 первое уравнение находим:
первое уравнение находим: 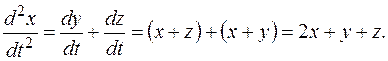
Исключаем переменные 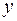 и z из уравнений
и z из уравнений
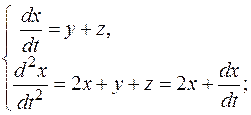
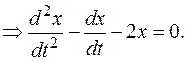
Получили линейное однородное дифференциальное уравнение с постоянными коэффициентами 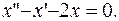 Решаем его через характеристическое уравнение
Решаем его через характеристическое уравнение
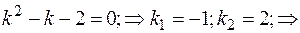 Решение однородного дифференциального уравнения:
Решение однородного дифференциального уравнения: 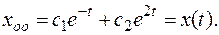
Находим 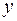 и
и 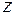 . Для чего сначала находим
. Для чего сначала находим 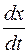 , дифференцируя
, дифференцируя 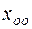 .
.
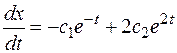 . Подставив в 1-е уравнение исходной системы, находим:
. Подставив в 1-е уравнение исходной системы, находим: 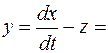
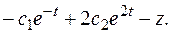
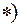
Из третьего уравнения исходной системы получаем:
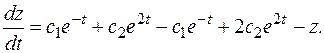
После преобразований получаем линейное дифференциальное уравнение 1-го порядка 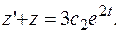 Решаем его методом Бернулли, выполнив замену:
Решаем его методом Бернулли, выполнив замену: 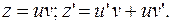
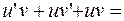
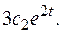
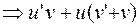
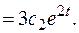
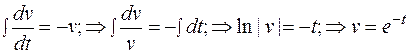 .
.
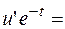
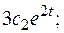

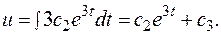
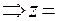
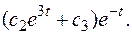
Подставив в 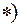 , получаем:
, получаем:
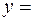
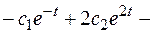
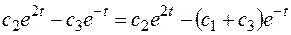 .
.
Таким образом, решение системы:

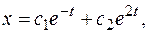
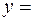
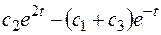 ,
,
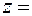
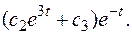
Существуют и другие методы решения систем дифференциальных уравнений.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1. Кремер Н.Ш. Высшая математика для экономистов. М.: ЮНИТИ, 1997.
2. Красс М.С. Математика для экономических специальностей. Учебник. М.: ИНФРА-М, 1998.
3.Ермаков В.И. Общий курс высшей математики для экономистов. Учебник. М.: ИНФРА-М, 2000.
4. Пискунов Н.С. Дифференциальное и интегральное исчисления. Для ВТУЗОВ. М.: Физматгиз,1963.
5. Гусак А.А. Справочное пособие к решению задач: математический анализ и дифференциальные уравнения. - Мн.: ТетраСистемс, 1998.
6.Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Часть 2. М.: Высшая школа,1980.
7.Ермаков В.И. Сборник задач по высшей математике для экономистов. Учебное пособие. М.: ИНФРА-М, 2001.
8.Малыхин В.И. Математика в экономике: Учебное пособие. - М.: ИНФРА-М, 2001
Дата добавления: 2020-10-25; просмотров: 753;











