Координаты центра тяжести площадей

В инженерных расчётах часто требуется определить центр тяжести плоской фигуры весом Р. Эта сила равномерно распределена по всей площади пластинки, так что G=А∙γ, где γ –сила тяжести, приходящаяся на единицу площади (вес 1м² площади).

Сила тяжести каждого участка:

G_i=A_i∙γ_i

A_i –площадь i-того участка.

Формулы координат центра тяжести площадей

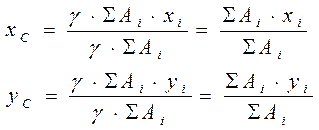
Центры тяжести простых фигур

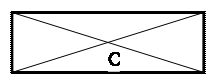
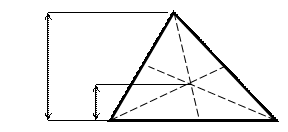
Прямоугольник С –точка пересечения диагоналей	Треугольник С –точка пересечения медиан
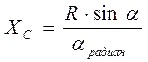
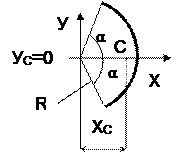
Дуга окружности	Круговой сектор 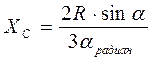При α=π/2 (полукруг)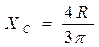

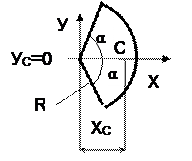
Алгоритм решения задач по методу разбиения

1. Разбиваем сечение на простейшие фигуры.

2. Показываем на чертеже центры тяжести каждой фигуры.

3. Выбираем оси отсчёта, если они не указаны.

4. Указываем на чертеже координаты центра тяжести каждой простейшей фигуры относительно осей отсчёта.

5. Находим площади и координаты центров тяжестей всех простейших фигур в отдельности.

6. Определяем координаты центра тяжести всей составной фигуры и показываем на чертеже точку С и её координаты.

1.2. Кинематика

Кинематика – раздел механики, занимающейся изучением движения материальных тел без учёта их масс и действующих на них сил.

Кинематику часто называют геометрией движения.

Механическое движение происходят в пространстве и во времени.

Время является скалярной, непрерывно изменяющейся величиной. В задачах кинематики оно принимается за независимую переменную, а все другие переменные величины рассматриваются как изменяющиеся с течением времени. Его отсчёт ведётся от некоторого начального момента t0=0 о выборе, которого уславливаются в каждом конкретном случае.

Положение движущегося тела в пространстве определяется по отношению к некоторому другому телу, принимаемому за систему отсчёта.

В природе не существует неподвижных тел и, следовательно, не может быть абсолютно неподвижных систем отсчёта. Обычно условно неподвижной системой отсчёта считают систему координаты осей, связанную с Землёй.

В зависимости от объекта, движение которого изучается, кинематику условно делят на:

- кинематику точки

- кинематику твёрдого тела

Движение любого объекта в кинематике считается заданным (указан закон, по которому можно определить положение объекта в пространстве по отношению к принятой системе отсчёта в любой момент времени).

Основная задача кинематики – определение кинематических характеристик движения (скорость, ускорение, пройденный путь и т.д.) по заданному движению объекта.

Траектория – непрерывная линия, которую описывает точка при движении.

По виду траектории движение точки может быть:

- прямолинейное

- криволинейное

Расстояние (дуговая координата)- длина участка траектории, отсчитанная от некоторой её неподвижной точки , принятую за начало отсчёта.

Отсчёт расстояний от начала траектории можно вести в обе стороны, поэтому S- величина алгебраическая, она может быть положительной или отрицательной.

Перемещение – вектор, соединяющий начальные и конечное положение точки.

Путь L – длина траектории, пройденная точкой за определенный промежуток времени (величина положительная).

Скорость – векторная величина, характеризующая в каждой данный момент времени направления и быстроту движения точки.

Ускорение – векторная величина, характеризующая быстроту изменения направления и модуля скорости.

1.2.2. Кинематика точки