Сложное движение твёрдого тела

Плоскопараллельным называется движение твёрдого тела, при котором все его точки движутся в плоскостях, параллельных некоторой неподвижной плоскости.

При изучении плоскопараллельного движения тела, достаточно рассматривать движение его любого сечения в плоскости xОy, в которой расположено сечение. На основании этого заключения рассмотрите вывод того, что плоскопараллельное движение тела – движение сложное и состоит из поступательного движения вместе с полюсом (выбранная в сечении тела произвольная точка) и вращательного движения вокруг полюса.

Поступательная часть плоскопараллельного движения характеризуется изменением с течением времени координат x и y полюса и изменением угла поворота φ сечения, т.е. закон плоскопараллельного движения можно задать тремя уравнениями:

x = f₁ (t ); y = f₂ (t ); φ = f ₃(t ).

Следует заметить, что первые два уравнения, описывающие поступательную часть плоскопараллельного движения, зависят от выбора полюса, а третье уравнение, описывающее вращательную часть, от выбора полюса не зависят.

Абсолютная скорость точки тела при плоскопараллельном движении равна геометрической сумме скорости полюса и относительной скорости этой точки вокруг полюса.

Мгновенный центр скоростей – это точка плоского сечения тела, абсолютная скорость которой равна нулю. Точка абсолютная скорость которой равна нулю, получила название мгновенного центра скоростей, потому что находится относительно выбранного полюса в положении, при котором абсолютная скорость равна нулю в течение малого промежутка времени.

Свойства мгновенного центра скоростей, вытекающие из закона распределения скоростей точек твёрдого тела, вращающегося вокруг неподвижной оси:

1) скорость мгновенного центра скоростей равна нулю;

2) мгновенный центр скоростей лежит на перпендикуляре, восстановленном из точки к направлению её скорости;

3) скорость любой точки равна произведению мгновенной угловой скорости на расстояние от точки до мгновенного центра скоростей.

Динамика

1.3.1 Основные понятия и аксиомы динамики

Динамика ­– это раздел теоретической механики, который изучает движение материальных тел под действием сил, то есть с учётом причин, вызвавших это движение.

Задачи динамики:

- прямая задача динамики сводится к определению реакций связей, если заданы закон движения точки и действующие на нее активные силы;

- обратная задача динамики сводится к тому, чтобы, зная действующие на точку активные силы, определить, во-первых, закон движения точки и, во-вторых, реакции связей.

В основе динамики лежат 4 закона, установленные Г.Галилеем и И.Ньютоном путем обобщения результатов многих опытов и наблюдений за движением тел.

Аксиома 1(принцип инерции). Всякая изолированная материальная точка находится в состоянии покоя или равномерного и прямолинейного движения, пока приложенные к ней силы не выведут её из этого состояния.

Аксиома 2 (основной закон динамики). Ускорение, сообщаемое точке силой, имеет направление силы и пропорционально её модулю.

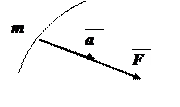
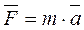В скалярной форме 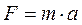где m – масса материальной точки – коэффициент пропорциональности, выражающий меру инертности материальной точки.

На все материальные тела вблизи Земли действует сила тяжести G, значение которой определяется произведением массы тела на ускорение свободного падения g.

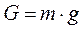
При свободном падении на Землю тела любой массы приобретают одно и то же ускорение g, которое называется ускорением свободного падения

Значение g=9,81м/с² зависит от географической широты местности и высоты над уровнем моря.

1Н – сила, сообщающая массе в 1кг ускорение 1 м/с².

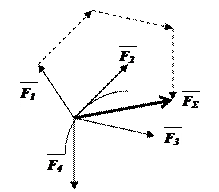
Аксиома 3 (закон независимости действия сил).

Если к материальной точке приложена система сил, то движение этой точки складывается из тех движений, которые точка могла бы иметь под действием каждой силы в отдельности. 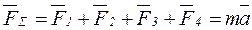[H]=[кг·м/с2] Разделим обе части равенства на массу m и получим:

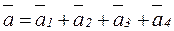
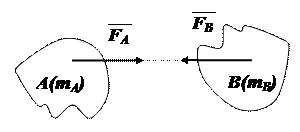
Аксиома 4 (закон равенства действия и противодействия). Две материальные точки действуют друг на друга с силами, равными по модулю и направленными в противоположные стороны.

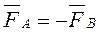
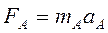
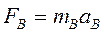
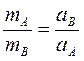
Четвертая аксиома в динамике имеет важное значение. Следует ясно представлять себе, что силы взаимодействия между двумя материальными точками не уравновешивают друг друга, так как одна сила приложена к одной точке, а вторая к другой.

1.3.2. Движение материальной точки. Метод кинетостатики