Угол и конус трения.

Полной реакцией опорной поверхности R называется равнодействующая силы трения R_f и силы нормального давления R_n.

Угол трения φ – это максимальный угол, на который отклонится от нормали к поверхности полная реакция опорной поверхности.

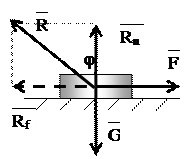
tg φ = R_f / R_n = f ∙ R_n / R_n

φ = arctg f

При отклонении реакции реальной связи угол φ её касательная составляющая достигает максимального значения max R_f, которая называется статической силой трения или силой трения покоя.

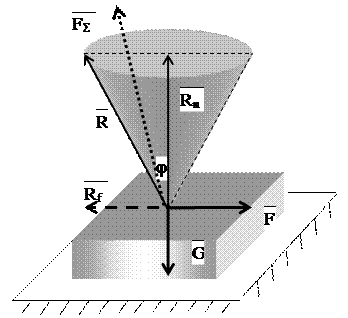
Так как сдвигающая сила F может действовать параллельно плоскости связи в любую сторону, то, если представить, что мы поворачиваем силу F вокруг нормали Rn, тогда отклонившаяся на постоянный угол φ реакция R, оставаясь, всё время в плоскости нормали и вектора F, образует конус, определяющий любое из возможных положений реакции R реальной связи. Этот конус называется конусом трения. Область, ограниченная конусом трения, определяет область равновесия тела.

Если равнодействующая всех сил попала в конус трения, то она не выведет тело из состояния равновесия (не сдвинет его). Сила, не попавшая в конус трения, всегда сдвинет тело.

 

Самоторможение: Если тело, опирающееся на шероховатую поверхность, под действием внешних сил находится в покое, то такое равновесие объясняется тем, что внешние силы не могут преодолеть силы трения, то есть наблюдается самоторможение.

 

Условие самоторможения: тело, лежащее на шероховатой поверхности, остаётся в покое до тех пор, пока линия действия равнодействующей активных сил, приложенных к телу, проходит внутри конуса трения.

Условие самоторможения наклонной плоскости:

α ≤ arctg f

Наклонная плоскость называется самотормозящей, если поставленное на неё тело не скользит под действием силы тяжести.

Трением качения называется сопротивление перекатыванию одного тела по поверхности другого. Сопротивление это вызвано главным образом тем, что как само катящееся тело, так и тело по которому оно катится, не являются абсолютно твёрдыми и поэтому всегда несколько деформируются в местах их соприкосновения.