Способы задания движения точки
а) Естественный: движение точки задаётся её траекторией и уравнением движения по этой траектории (законом движения)
S = f (t)
где S – расcтояние точки от начального положения, t – время движения точки от начального момента.
Положение точки в любой момент времени определяется подстановкой t в уравнение
Пример: S=5t²
При t0=0; S0=0 – точка находится в начале отсчёта
t1=1c; S1=5м
б) Координатный: положение точки в пространстве определяется координатами x, y, z; на плоскости x, y.

x=f1(t)
y=f2(t)
z=f3(t)
Подставив в эти уравнения время, можно определить положение проекций точки в любой момент времени.
Для определения уравнения траектории y=f(x),необходимо из уравнений движения исключить время.
Пример: x=8t+20
y=5t
Решение: t=y/5; x=8y/5+20=1,6y+20. Траектория – прямая линия.
Скорость точки
Если точка, за равные промежутки времени, проходит равные отрезки пути, то её движение называется равномерным, если неравные – неравномерным.
V=S/t – равномерное движение
[км/ч; м/с] 1 км/ч = 0,278 м/с
1м/с =3,6 км/ч
Скорость неравномерного движения – величина переменная V=f(t)
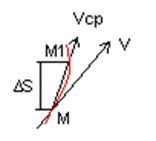 Рассмотрим точку, движение которой задано уравнением S=f(t). За промежуток времени ∆t т. М переместиться в положение М1 по дуге ММ1, пройдя путь ∆S.
Рассмотрим точку, движение которой задано уравнением S=f(t). За промежуток времени ∆t т. М переместиться в положение М1 по дуге ММ1, пройдя путь ∆S.
Средняя скорость движения точки
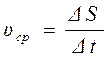
(Если промежуток времени ∆t мал, то дугу можно заменить хордой) средняя скорость направлена по хорде от т. М к М1.
Скорость в данный момент времени найдём путём перехода к пределу ∆t→0.
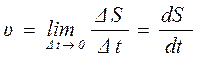
Мгновенная скорость при любом движении точки равна первой производной координаты по времени.
Скорость в каждый момент времени направлена по касательной к траектории в сторону движения
Пример: S = 0,1t²+t
V = dS/dt = 0,2t+1
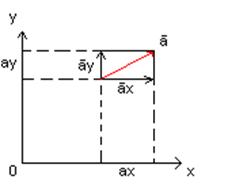
При координатном способе движения точки, определяют проекции скорости на координатные оси.
Проекция скорости на координатную ось равна первой производной от соответствующей координаты по времени.
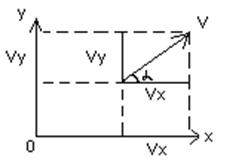
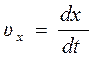

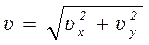
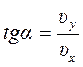
cos(V^,x) = Vx/V
cos(V^,y) = Vy/V
3. Ускорение точки
Это изменение скорости в единицу времени.
При прямолинейном движении точки вектор скорости совпадает с траекторией, следовательно, и вектор изменения скорости совпадает с траекторией.
Среднее ускорение aср = ∆V/∆t
Истинное ускорение в прямолинейном движении равно первой производной скорости или второй производной координаты по времени, (м/с²).

При движении точки по криволинейной траектории скорость меняет своенаправление.
Ускорение точки равно векторной производной скорости по времени.
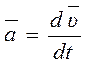
а) Естественный способ
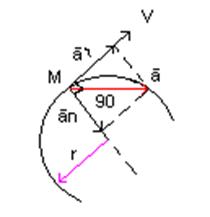 Для удобства полное ускорение раскладывают на две взаимно перпендикулярные составляющие по касательной и нормали к траектории движения
Для удобства полное ускорение раскладывают на две взаимно перпендикулярные составляющие по касательной и нормали к траектории движения
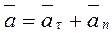
aτ – касательное (тангенциальное) ускорение совпадает по направлению со скоростью или противоположно ей; характеризует изменение модуля скорости
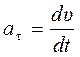
ān – нормальное (центростремительное) ускорение перпендикулярно к направлению скорости точки; определяет изменение направления вектора скорости.
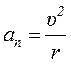
где r – радиус кривизны траектории
Нормальное ускорение направлено по нормали к центру кривизны траектории.
Полное ускорение точки
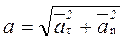
б) Координатный способ
Проекция ускорения на координатную ось равна второй производной от соответствующей координаты по времени

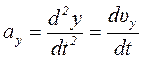
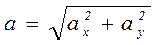
Дата добавления: 2020-10-14; просмотров: 1070;











