Представление формул
Формула – это комбинация математических или химических знаков, выражающих какое-либо предложение.
Формулы рекомендуется оформлять в редакторе формул (стиль текст, размер 14). Они располагаются отдельными строками с выравниванием по центру.
В формулах в качестве символов следует применять обозначения, установленные соответствующими государственными стандартами. Пояснения символов и числовых коэффициентов, входящих в формулу, если они не пояснены ранее, должны быть приведены непосредственно под формулой. Пояснения каждого символа следует давать с новой строки в той последовательности, в которой символы приведены в формуле. Первая строка пояснения должна начинаться со слова «где» без двоеточия после него.
Пример:
Глубина заложения оси нефтепровода Н3, м,
Н3 = Dн / 2 + 800,
| где | Dн | – | наружный диаметр трубопровода, мм, Dн=1220 мм, [1] |
Н3 = 1220 / 2 + 800 = 1410 мм.
Секундный расход при расчетной температуре Qc, м3/с,
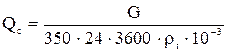 ,
,
| где | G | – | объём годовой перекачки, т/год, G = 98·106 т/год; |
| rt | – | плотность нефти при расчетной температуре, кг/м3, |
rt = r20 – x×( 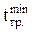 – 20),
– 20),
| где | r20 | – | плотность ромашкинской нефти при температуре 20°С, r20, кг/м3, r20 = = 864 кг/м3; [2] |
| x | – | температурная поправка, кг/м3·°С, |
ξ = 1,825 – 0,001315·ρ20,
ξ = 1,825 – 0,001315·864 = 0,689 кг/м3·°С,
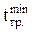
| – | минимальная температура грунта, °С, 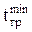 = 3°С; = 3°С;
|
r3 = 864 –0,689×(3 – 20) = 875,71 кг/м3,
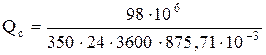 =3,7 м3/с.
=3,7 м3/с.
Формулы, следующие одна за другой и не разделенные текстом, разделяют запятой.
Переносить формулы на следующую строку допускается только на знаках выполняемых операций, причем знак в начале следующей строки повторяют. При переносе формулы на знаке умножения применяют знак « 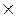 ».
».
Формулы, за исключением формул, помещаемых в приложении, должны нумероваться сквозной нумерацией арабскими цифрами, которые записывают на уровне формулы справа в круглых скобках. Одну формулу обозначают – (1).
Ссылки в тексте на порядковые номера формул дают в скобках.
Например: подставив соответствующие значения в формулу (1).
Порядок изложения в документах математических уравнений такой же, как и формул.
Дата добавления: 2016-07-22; просмотров: 1919;











