Основное уравнение насоса (уравнение Эйлера)

Напор, развиваемый насосом, и коэффициент полезного действия тесно связан со значением и направлением скоростей потока жидкости в межлопастных каналах колеса. Для установления этой связи воспользуемся классической теоремой об изменении моментов количества движения, которая может быть сформирована следующим образом: производная по времени главного момента количества движения системы материальных точек относительно некоторой оси равна сумме моментов всех внешних сил, действующих на эту систему. Математически теорема записывается следующим образом:

d[(mυ)r] / dt = ΣM

где m – масса рассматриваемой системы материальных точек;

υ – абсолютная скорость их движения;

r – расстояние до оси.

Удобство теоремы об изменении моментов количества движения в приложении к сплошной среде заключается в том, что с ее помощью динамическое взаимодействие между жидкостью и обтекаемыми поверхностями можно определить по характеру течения в контрольных сечениях без учета структуры потока внутри выделенного объема.

При подаче насоса Q масса жидкости, участвующей в движении, составляет: m = ρQ, где ρ – плотность жидкости.

Момент количества движения на выходе из колеса:

M_к.д.2 = ρQυ₂r_вых

Момент количества движения жидкости на входе в колесо

M_к.д.1 = ρQυ₁r_х

С учетом сделанных допущений это уравнение может быть переписано в виде:

ΣM = M_к.д.2 - M_к.д.1 = ρQ(υ₂r_вых - υ₁r_вх)

Из треугольников скоростей следует, что

r_вх = D₁cos α₁ / 2

r_вых = D₂cos α₂ / 2

где D₁ – диаметр всаса, D₂ – диаметр рабочего колеса.

Нарисуем параллелограммы скоростей потока на входе в рабочее колесо центробежного насоса и на выходе из него.

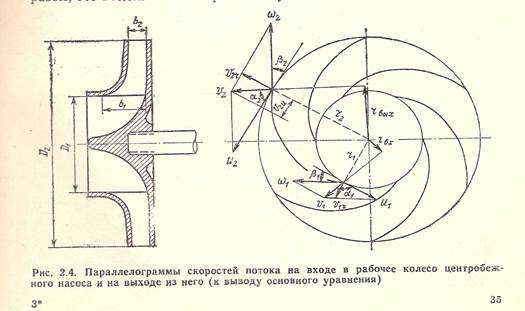
Подставляя значение r_вых и r_вх , получим:

ΣM = ρQ(υ₂r_вых*D₂/2 - υ1rвх*D₁/2)

Все внешние силы, действующие на массу жидкости, заполняющей межлопастные каналы рабочего колеса, можно разделить на три группы:

1) Сила тяжести.

2) Давление на жидкость.

3) Силы на обтекаемых поверхностях рабочего колеса.

Таким образом, момент всех внешних сил относительно оси вращения сводятся к моменту динамического воздействия рабочего колеса M_р.к. на протекающую через него жидкость, т.е.

ΣM = M_р.к.

При этом, мощность, передаваемая жидкости рабочим колесом насоса, равна произведению M_р.к. ω = ρgQH_т

где H_т – теоретический напор, создаваемый рабочим колесом насоса.

H_т = (u₂υ₂cos α₂ – u₁υ₁cos α₁) / g

Эта зависимость была впервые выведена в середине 18 века математиком и механиком Леонардом Эйлером, членом Петербургской академии. Она получила название уравнение Эйлера или основное уравнение лопастного насоса.