Движение жидкости внутри рабочего колеса центробежного насоса (треугольники скоростей на входе и выходе из рабочего колеса)»

Преобразование подводимой к насосу механической энергии в энергию движущейся жидкости в лопастных насосах производится за счет непосредственного силового воздействия лопастей рабочего колеса на жидкость, заполняющую его каналы. Рабочее колесо является основным элементом насоса, а кинематические показатели (значения и направление скоростей, траектория движения и т.п.) движущейся через колесо жидкости оказывают решающее влияние на энергетические параметры колеса (напор, подача, КПД).

Жидкость, проходя через колесо, совершает сложное движение: она входит в колесо в направлении, параллельном оси вала, а выходит перпендикулярно оси. При этом каждая частица жидкости вращается вместе с колесом с окружной скоростью υ и одновременно перемещается вдоль лопатки с относительной скоростью ω. Согласно общим положениям механики жидкости, абсолютная скорость υ в области лопастного колеса может быть получена как геометрическая сумма относительной ω и переносной u скоростей. В векторной форме: υ=ω+ū

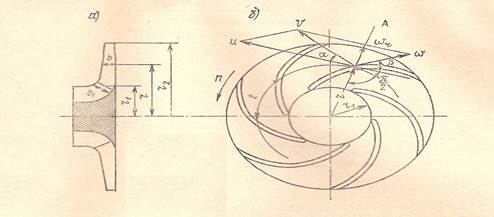
Параллелограмм скоростей потока в рабочем колесе центробежного насоса.

В основу представления об установившемся движении потока через рабочее колесо центробежного насоса положена гипотеза о струйном течении жидкости. Согласно этой гипотезе траектория каждой частицы жидкости в пределах межлопастного канала колеса по форме совпадает с кривой очертания лопасти.

Предположим, что заданы геометрические размеры рабочего колеса центробежного насоса (рис. а), его объемная подача Q и частота вращения n. Определим, пользуясь гипотезой о струйном течении, значения и направления относительной скорости на плоском сечении колеса, перпендикулярном оси насоса в некоторой точке потока, отстоящей от оси вращения на расстоянии r (рис. б). Для определения значения относительной скорости воспользуемся уравнением неразрывности, составив его для цилиндрического сечения потока, проходящего через рассматриваемую точку. Площадь этого сечения обозначим через f_r. Радиальная составляющая скорости потока

ω_r=Q/ f_r

Учитывая коэффициентом ψ стеснение сечения телом лопастей шириной b, получим:

f_r=2πrbψ

ω_r=Q/2πrbψ

Переносная скорость в рассматриваемой точке потока равна окружности скорости вращения колеса

u= ω=(2πrn)/60

и направлена по касательной к окружности радиусом r в сторону вращения.

Радиальная составляющая относительной скорости ω_r перпендикулярна вектору переносной скорости u. Касательная к поверхности лопасти, по которой направлена относительная скорость ω образует угол β с направлением обратным переносной скорости. Проведя из конца вектора ω_r прямую, параллельную направлению скорости u, до пересечения с этой касательной, получим, согласно плану скоростей, в этой точке пересечения конец вектора относительной скорости ω. Значение относительной скорости:

ω= ω_r/sin β =Q/(2πrbψ sin β)

Суммируя по правилу параллелограмма относительную и переносную скорость, получим полную скорость. Поскольку радиальная составляющая ω_r относительной скорости равна радиальной составляющей υ_r абсолютной скорости, то значение скорости υ может быть определена из соотношения:

υ= υ_r/sinα=Q/(2πrbψsinα)

где α – угол между направлениями абсолютной и переносной скоростей.

Таким образом, гипотеза о струйном течении жидкости, основанная на предположении о бесконечном числе лопастей, позволяет построить параллелограмм скоростей в любой точке внутри рабочего колеса насоса.

Коэффициент стеснения ψ равен отношению действительной площади сечения потока к площади сечения свободного от лопастей:

ψ=(2πrb – zbs)/ 2πrb

где z – число лопастей, s – толщина лопастей в рассматриваемом цилиндрическом сечении.

Обозначая через t=2πr/z шаг, расстояние по окружности между одноименными точками смежных лопастей, получим, что коэффициент стеснения

ψ=(t – s)/t

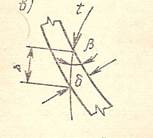
Толщина лопасти s может быть выражена через нормальную толщину δ и угол β

S= δ/sin β

Величина окружной составляющей абсолютной скорости u жидкости характеризует закрутку жидкости на входе в рабочее колесо u₁ и на выходе u₂. На входе в рабочее колесо закрутка жидкости может отсутствовать u₁=0 или u₁≠0, при этом она направлена в сторону вращения (положительная) и против вращения (отрицательная). Закрутка потока применяется с целью улучшения антикавитационных свойств насоса. Закрутка в сторону вращения рабочего колеса способствует увеличению всасывания жидкости насосом, против вращения насоса – увеличение напора.

Построим треугольники скоростей на входе и выходе в рабочем колесе насоса.

При построении треугольников скоростей осевых насосов следует учитываьб две особенности:

1) Скорости переносного движения всех точек лопастей рабочего колеса в том числе входной и выходной кромок для рассматриваемого цилиндрического слоя, определяя по формуле: u=u₁= u₂=2πr_in/60

2) В силу сплошности потока осевые составляющие абсолютной скорости υ во всех точках рассматриваемого цилиндрического слоя должна быть:

υ_z= υ sinα = υ₁sinα₁ = υ₂sinα₂

υ_z=ω sinβ = ω₁sinβ₁ = ω₂sinβ₂

υ_z= ΔQ/2πr_iΔr_i = 4Q/π(D² – d²_вт)

где D – внешний диаметр рабочего колеса, d_вт – диаметр втулки.

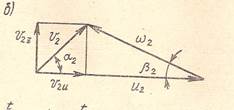
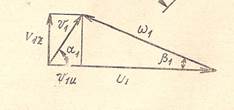
Таким образом, треугольники скоростей на входной и выходной кромках лопастей имеют одинаковое основание и равную высоту.

Принципиальное отличие работы решетки профилей от единичного профиля заключается в том, что направления скорости жидкости до и после решетки различны, т.к. решетка профилей меняет направление скорости на бесконечности, а единичный профиль этого направления не меняется.