Зразок виконання завдання
| 
|
| 
|
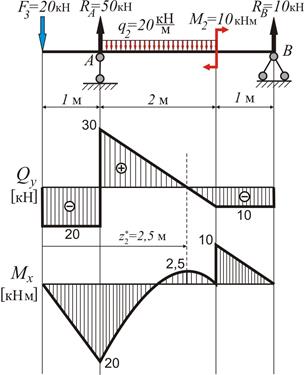
Розрахунок на міцність балки 4:
1. Визначення реакцій опор:
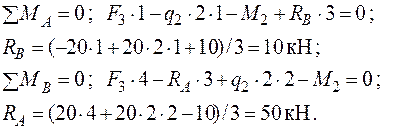
Перевірка: 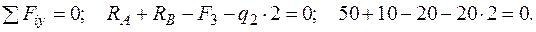
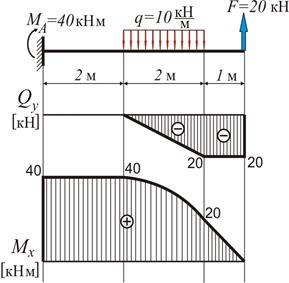
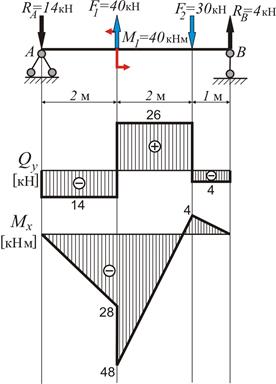
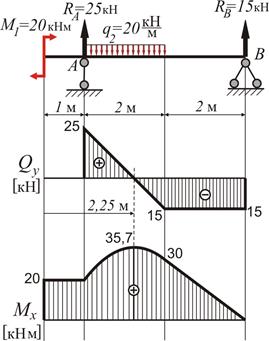
2. Визначення поперечних зусиль Qy та моментів згину Mx :
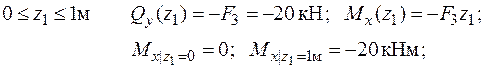
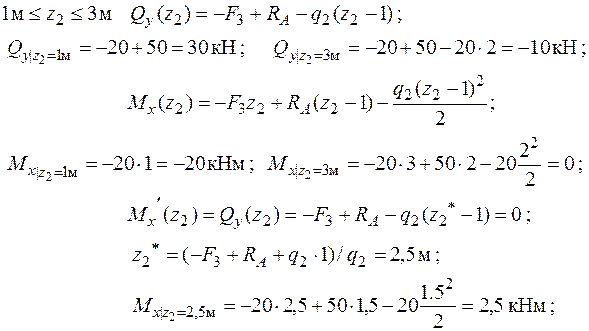
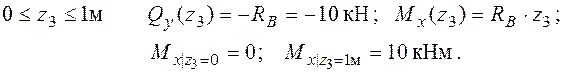
3. Підбір перерізів з умови міцності:
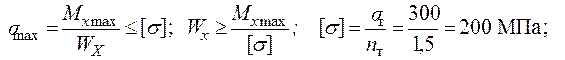
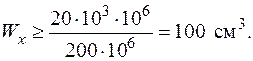
Для двотавра згідно з додатком 4 приймаємо Ι №16: 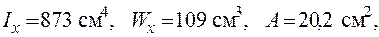
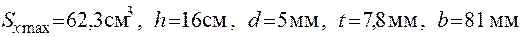 .
.
Як відомо, для прямокутного перерізу 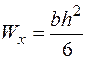 , тоді
, тоді
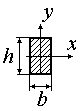
| при відношенні сторін прямокутника
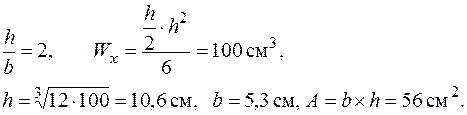
|
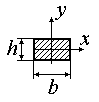
| Для прямокутника з відношенням сторін
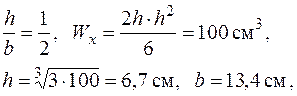
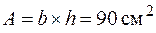 . .
|
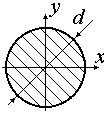
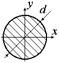
| Для круга
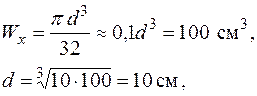
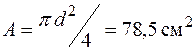 . .
|
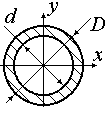
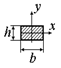
| Для кільця
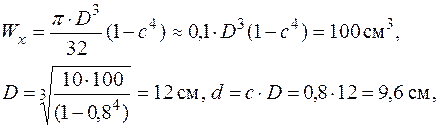 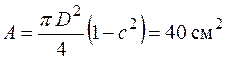 .
Зробимо порівняльний аналіз перерізів: .
Зробимо порівняльний аналіз перерізів:
| |||||||
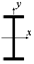
| 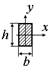
| 
| 
| 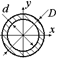
| ||||
| Аi,см2 | 20,2 | 78,5 | ||||||
| Аi/Аmin | 2,8 | 4,5 | 3,9 | |||||
4. Визначимо нормальні та дотичні напруження у двотаврі
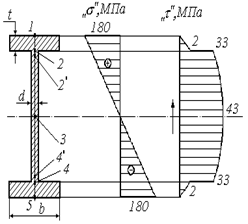
| 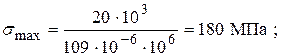
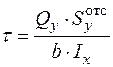 ; ; 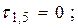 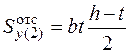 ; ;
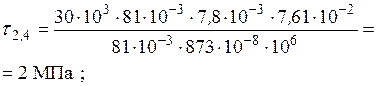
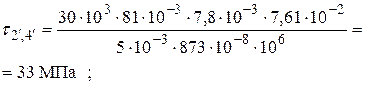
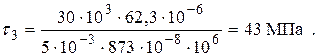
|
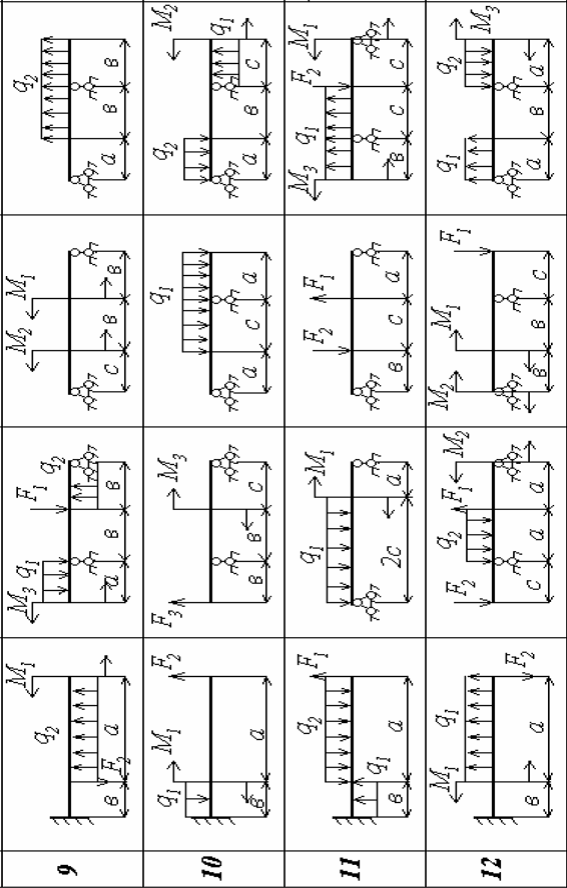
Додаток 2.1 − Розрахункові схеми
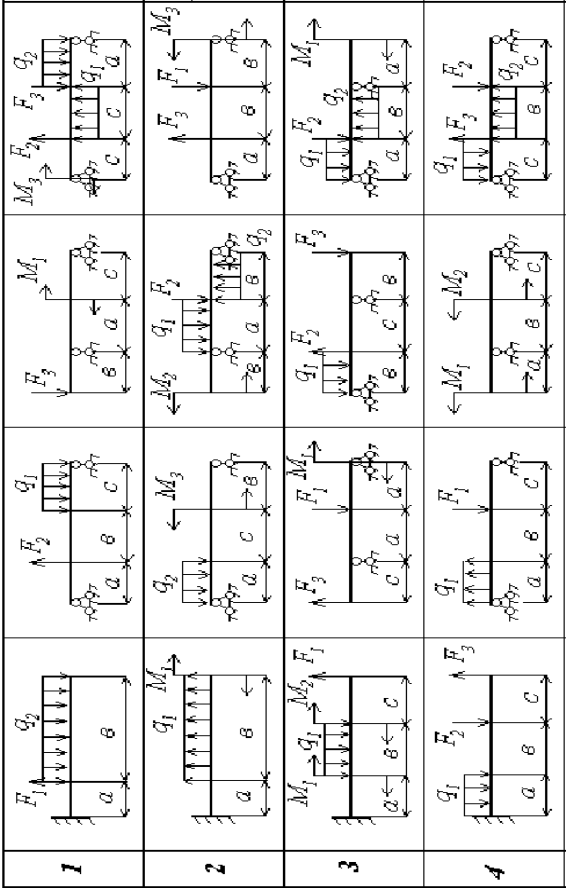
| |||||
| Продовження додатка 2.1 | |||||
 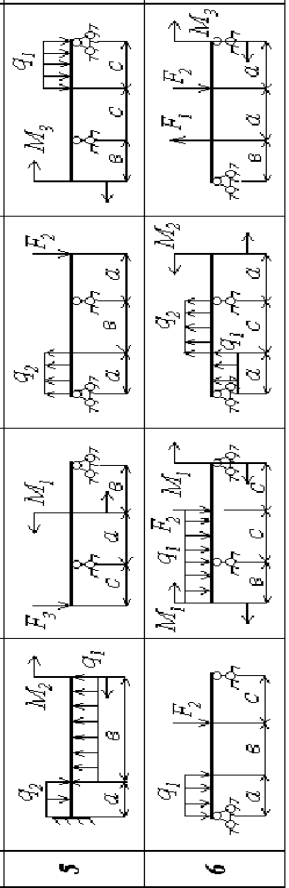
| |||||
| Продовження додатка 2.1 | |||||
| |||||
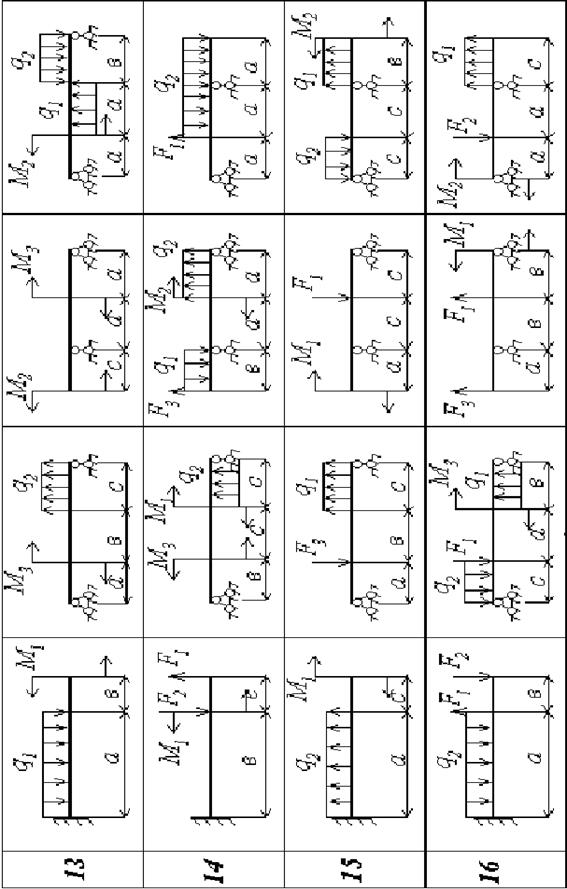
| Продовження додатка 2.1 | |||||
| |||||
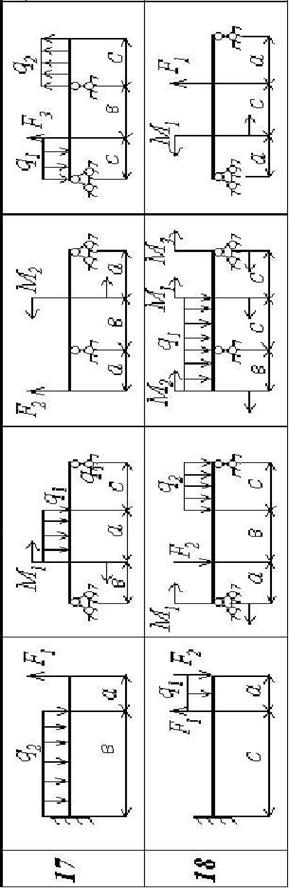
| Продовження додатка 2.1 | |||||
| |||||
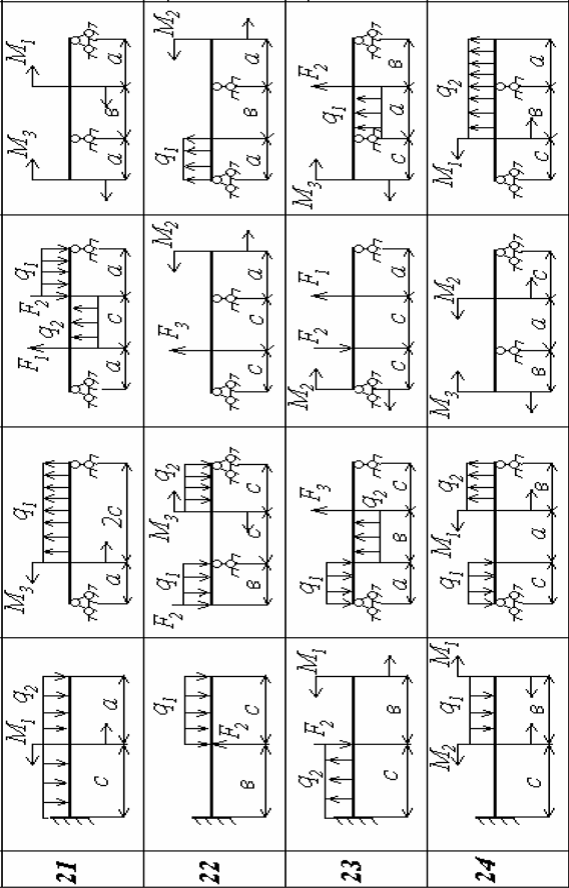
| Продовження додатка 2.1 | |||||
| |||||
Додаток 2.2 − Вхідні дані
| Варіант | 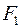
| 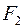
| 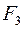
| 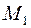
| 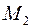
| 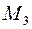
| 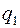
| 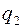
| 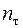
| 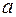
| 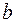
| 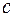
|
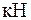
| 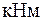
| 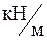
| 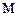
| |||||||||
| 1. | 1,7 | 1,5 | 1,0 | 2,0 | ||||||||
| 2. | 1,4 | 2,0 | 2,5 | 2,0 | ||||||||
| 3. | 1,5 | 1,5 | 1,5 | 2,0 | ||||||||
| 4. | 1,6 | 2,5 | 2,5 | 1,5 | ||||||||
| 5. | 1,8 | 2,0 | 2,0 | 2,0 | ||||||||
| 6. | 2,0 | 1,5 | 2,0 | 2,5 | ||||||||
| 7. | 1,8 | 2,5 | 3,0 | 2,0 | ||||||||
| 8. | 1,6 | 2,0 | 2,0 | 2,0 | ||||||||
| 9. | 1,5 | 1,0 | 1,5 | 2,5 | ||||||||
| 10. | 1,4 | 1,5 | 2,5 | 2,0 | ||||||||
| 11. | 1,6 | 1,5 | 2,0 | 2,5 | ||||||||
| 12. | 1,4 | 2,5 | 3,0 | 2,0 | ||||||||
| 13. | 1,5 | 1,0 | 2,5 | 3,0 | ||||||||
| 14. | 1,6 | 1,5 | 1,2 | 2,5 | ||||||||
| 15. | 1,8 | 2,5 | 2,0 | 1,5 | ||||||||
| 16. | 1,7 | 1,5 | 1,0 | 2,0 | ||||||||
| 17. | 1,4 | 2,0 | 2,5 | 2,0 | ||||||||
| 18. | 1,5 | 1,5 | 1,5 | 2,0 | ||||||||
| 19. | 1,6 | 2,5 | 2,5 | 1,5 | ||||||||
| 20. | 1,8 | 2,0 | 2,0 | 2,0 | ||||||||
| 21. | 2,0 | 1,5 | 2,0 | 2,5 | ||||||||
| 22. | 1,8 | 2,5 | 3,0 | 2,0 | ||||||||
| 23. | 1,6 | 2,0 | 2,0 | 2,0 | ||||||||
| 24. | 1,5 | 1,0 | 1,5 | 2,5 |
Примітка. Матеріал − сталь Ст. 30: 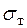 = 300 МПа.
= 300 МПа.
Додаток 2.3 − Основні поняття, позначення, формули, формулювання та правила з теми «Згинання стержнів»
| Позначення та формули | Одиниця виміру | Назва |
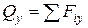
| Н (ньютон) | внутрішня поперечна сила |
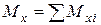
| Нм | внутрішній згинальний момент |
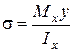
| Па (паскаль) | нормальне напруження |
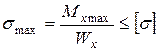
| Па | умова міцності за нормальними напруженнями |
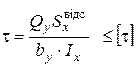
| Па | умова міцності за дотичними напруженнями |
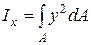
| м4 | осьовий момент інерції |
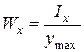
| м3 | осьовий момент опору |
Поперечна сила в даному перерізі – 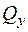 чисельно дорівнює алгебраїчній сумі проекцій на нормаль (вісь Y) до осі стержня сил, розташованих по одну сторону від перерізу (всіх однобічних сил), та утворює заміну діі відкинутої частини на залишену.
чисельно дорівнює алгебраїчній сумі проекцій на нормаль (вісь Y) до осі стержня сил, розташованих по одну сторону від перерізу (всіх однобічних сил), та утворює заміну діі відкинутої частини на залишену.
Згинальний момент 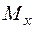 в даному перерізіz – чисельно дорівнює алгебраїчній сумі моментів щодо поперечної осі перерізу сил, які розташовані по одну сторону від цього перерізу (всіх однобічних сил).
в даному перерізіz – чисельно дорівнює алгебраїчній сумі моментів щодо поперечної осі перерізу сил, які розташовані по одну сторону від цього перерізу (всіх однобічних сил).
Правила знаків:
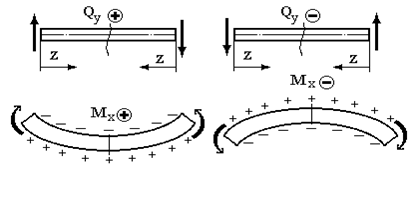
Контрольні питання
1. Що називається згинанням балок?
2. Класифікація згинання.
3. Як знайти внутрішній згинальний момент у довільному перерізі балки?
4. Правило знаків для згинального моменту.
5. Як знайти внутрішню поперечну силу в довільному перерізі балки?
6. Правило знаків для поперечної сили.
7. Диференційні залежності при згинанні.
8. Правила побудови та перевірки епюр внутрішніх силових факторів.
9. Як визначити нормальні напруження при чистому згинанні?
10. Що таке нейтральна лінія і де вона знаходиться?
11. У яких точках перерізу виникають максимальні нормальні напруження?
12. Умова міцності по нормальним напруженням при згинанні.
13. Яку форму мають раціональні перерізи при згинанні?
14. Як визначити дотичні напруження при поперечному згинанні?
15. У яких точках перерізу виникають максимальні дотичні напруження?
16. Умова міцності по дотичним напруженням при згинанні.
Кручення
В даному розділі посібника розглядаються два основних види деформації стержня: зсув (зріз) та кручення.
Зсув або зріз виникає тоді, коли зовнішні сили зміщують два паралельні плоскі перерізи стержня один відносно одного при незмінній відстані між ними.
Кручення виникає при дії на стержень зовнішніх сил, які утворюють момент відносно осі стержня. Деформація кручення супроводжується поворотом поперечних перерізів стержня один відносно одного навколо його осі.
Зсув
Деформація зсуву відбувається тоді, коли з шести компонент головного вектора сил та головного вектора моменту внутрішніх зусиль не дорівнюють нулю тільки поперечні сили 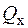 або
або 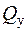 .
.
Дата добавления: 2020-10-14; просмотров: 546;











