Розподіл дотичних напружень для двотаврового перерізу
В перерізі діють згинальний момент Мх та поперечна сила  (рис. 2.17). Використовуючи вираз (2.13) для дотичних напружень, визначимо
(рис. 2.17). Використовуючи вираз (2.13) для дотичних напружень, визначимо
їхні значення в характерних точках перерізу. З достатнім ступенем точності можна замінити реальну форму полиці і стінки на прямокутники.
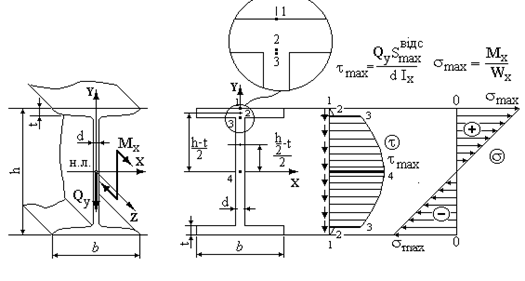
Рисунок 2.17
Точка 1: 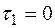 , тому що
, тому що 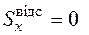 (вище рівня 1 відсічена площа відсутня).
(вище рівня 1 відсічена площа відсутня).
Точки 2, 3. Ці точки мають однакову координату y, але належать полиці та стінці одночасно, тобто різній ширині b2=b; b3=d. Тому в місці переходу полки в стінку виникає скачок дотичних напружень.
Точка 2 (приналежна полиці):
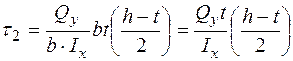 .
.
Точка 3 (приналежна стінці):
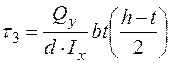 .
.
Точка 4:
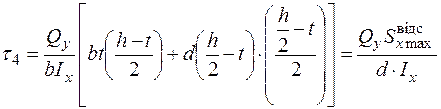 .
.
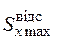 − статичний момент щодо центральної осі половини площі перерізу (для стандартних профілів приведений у таблицях сортаменту). Графік розподілу дотичних напружень приведено на рис. 2.17.
− статичний момент щодо центральної осі половини площі перерізу (для стандартних профілів приведений у таблицях сортаменту). Графік розподілу дотичних напружень приведено на рис. 2.17.
Порядок виконання проектувального розрахунку
При згинанні
1. З умови міцності по нормальним напруженням визначаємо осьовий момент опору поперечного перерізу, тобто 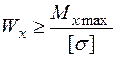 , та проектуємо переріз.
, та проектуємо переріз.
2. Перевіряємо переріз по дотичним напруженням. Якщо 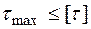 , то розрахунок закінчений. Якщо
, то розрахунок закінчений. Якщо 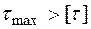 (перевищення більш 5%), то розміри перерізу визначаються з умови міцності по дотичним напруженням.
(перевищення більш 5%), то розміри перерізу визначаються з умови міцності по дотичним напруженням.
Приклад 1. Визначити розміри двотаврового поперечного перерізу балки (рис. 2.18), якщо допустиме нормальне напруження 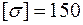 МПа, дотичне –
МПа, дотичне – 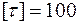 МПа.
МПа.
1. Визначаємо реакції:
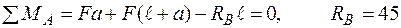 кН;
кН; 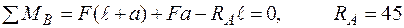 кН.
кН.
Перевірка: 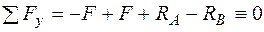 .
.
2. Розбиваємо балку на три ділянки та записуємо для поточного перерізу на кожній ділянці вирази для  і
і  :
:
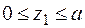 ;
; 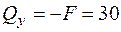 кН;
кН; 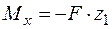 ;
;
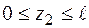 ;
; 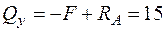 кН;
кН; 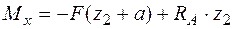 ;
;
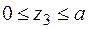 ;
; 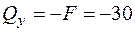 кН;
кН; 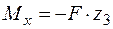 .
.
Обчислюємо  і
і  в характерних перерізах та будуємо епюри.
в характерних перерізах та будуємо епюри.
3. З побудованих епюр видно, що небезпечними є перерізи на обох опорах (де 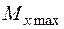 =24 кНм), та будь-який переріз на консолях
=24 кНм), та будь-який переріз на консолях
(де 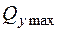 =30 кН).
=30 кН).
4. З умови міцності по нормальним напруженням визначаємо осьовий момент опору: 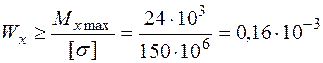 м3 = 160см3.
м3 = 160см3.
По таблицях ГОСТ 8239−89 обираємо двотавр №18а, для якого 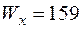 см3, що незначно менше розрахункового значення.
см3, що незначно менше розрахункового значення.
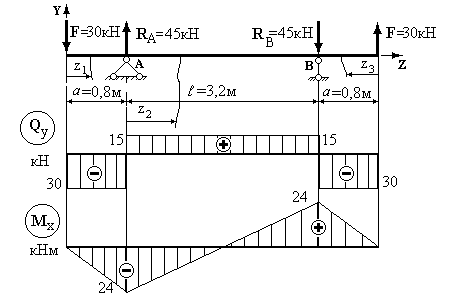
Рисунок 2.18
Інші необхідні для розрахунку параметри двотавру: 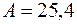 см2 ,
см2 , 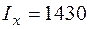 см4 ;
см4 ; 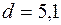 мм,
мм, 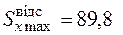 см3.
см3.
5. Перевіряємо виконання умови міцності по дотичним напруженням:
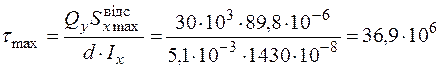 Па =36,9 МПа < [t].
Па =36,9 МПа < [t].
Умова міцності виконується і розрахунок закінчено.
Приклад 2. Для даної схеми навантаження дерев'яної балки перекриття (рис. 2.19) визначити розміри прямокутного перерізу, якщо відношення сторін прямокутника 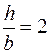 ; допустиме нормальне напруження
; допустиме нормальне напруження 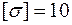 МПа, дотичне
МПа, дотичне 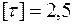 МПа. Оскільки навантаження симетричне, опорні реакції однакові і дорівнюють половині зовнішнього навантаження, тобто
МПа. Оскільки навантаження симетричне, опорні реакції однакові і дорівнюють половині зовнішнього навантаження, тобто 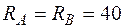 кН.
кН.
1. Визначаємо поперечні сили та згинальні моменти по ділянкам.
Перша ділянка: 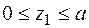 ; Þ
; Þ 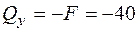 кН;
кН;  .
.
Друга ділянка: 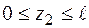 ; Þ
; Þ 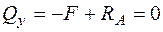 ;
; 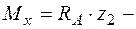
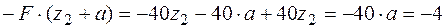 кНм.
кНм.
Третя ділянка: 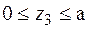 ; Þ
; Þ 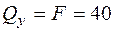 кН;
кН; 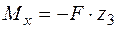 .
.
З епюр (рис. 2.9) видно, що небезпечними є перерізи на обох опорах, де  та
та  одночасно приймають максимальні значення
одночасно приймають максимальні значення
( 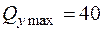 кН,
кН, 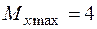 кНм).
кНм).
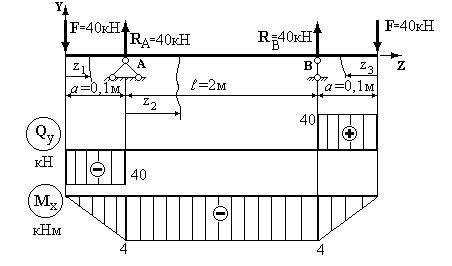
Рисунок 2.19
2. З умови міцності по нормальним напруженням знаходимо осьовий момент опору перерізу:
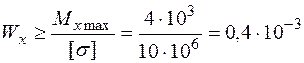 м3 = 400 см3.
м3 = 400 см3.
Як відомо, для прямокутника 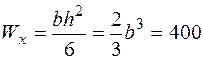 см3,
см3,
звідки обчислюємо розміри його сторін та площу:
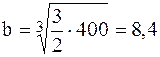 см,
см, 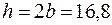 см,
см, 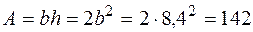 см2
см2
3. Перевіримо виконання умови міцності по дотичним напруженням. Максимальне дотичне напруження для прямокутного перерізу дорівнює: 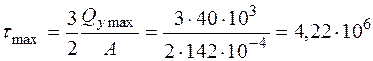 Па = 4,22 МПа , що перевищує допустиме напруження [t]=2,5МПа – умова міцності не виконується.
Па = 4,22 МПа , що перевищує допустиме напруження [t]=2,5МПа – умова міцності не виконується.
Визначаємо розміри поперечного перерізу з умови міцності по дотичним напруженням: 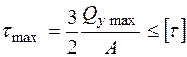 , звідки знаходимо площу поперечного перерізу:
, звідки знаходимо площу поперечного перерізу: 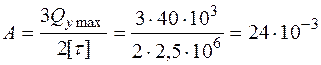 м2 = 240 см2 . Площа
м2 = 240 см2 . Площа 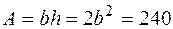 см2, звідки ширина перерізу:
см2, звідки ширина перерізу: 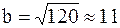 см, а висота
см, а висота 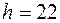 см. Таким чином, умова міцності по дотичним напруженням виявилась більш строгою, тому остаточно обираємо такі сторони прямокутника:
см. Таким чином, умова міцності по дотичним напруженням виявилась більш строгою, тому остаточно обираємо такі сторони прямокутника: 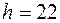 см,
см, 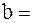 11 см.
11 см.
Дата добавления: 2020-10-14; просмотров: 697;











