Кільцевого перерізів

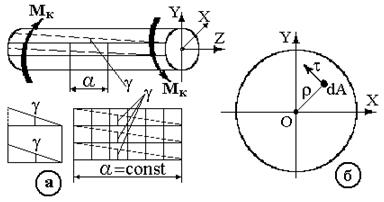
На валу з круглим перерізом (рис. 3.8 а) відзначимо утворюючі (меридіани) та поперечні перерізи (паралелі) та розглянемо експериментальні результати його кручення:

	Рисунок 3.8

1. При крученні поперечні перерізи стержня повертаються навколо його осі і відносно один одного.

2. Утворюючі повертаються на один і той же кут 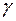. Прямокутники перетворюються в паралелограми, прямі кути змінюються, як і у випадку чистого зсуву (рис. 3.8 а). Це свідчить про те, що виділений елементарний обсяг будь-якого шару вала знаходиться в умовах чистого зсуву.

3. При крученні стержня круглого перерізу дотримується гіпотеза плоских перерізів: переріз плоский і нормальний до осі перед деформуванням залишається плоским і нормальним до осі в процесі деформівання.

4. Відстані між перерізами в процесі деформації не змінюються ( 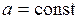), це підтверджує відсутність у перерізі нормальних напружень.

5. Довжина і прямолінійність радіусів перерізів не порушується, тобто дотичні напруження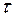у будь-якій точці перерізу перпендикулярні радіусу 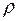(рис. 3.8 б).

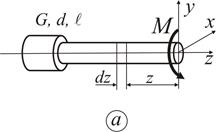
Розглянемо стержень діаметром 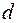, довжиною 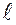, що навантажений моментом 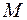(рис. 3.9 а). На відстані 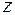від правого краю виділимо елемент довжиною 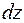і розглянемо його рівновагу (рис. 3.9 б).

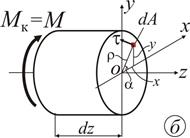
Вважаючи, що початок координат співпадає з центром ваги О перерізу, запишемо рівняння статичної рівноваги елементу :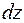

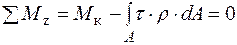. (3.5)

Рисунок 3.9

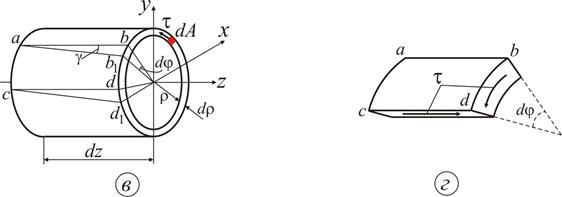
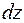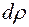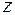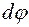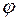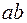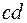Проведемо геометричний аналіз деформацій при крученні. Для цього з нескінченно малої ділянки вала довжиною виділимо трубку, перерізом якої є нескінченно тонке кільце товщиною (рис. 3.9 в). Умовно вважаємо, що лівий переріз нерухомий. Правий переріз повернеться навколо осі на кут , причому назвемо абсолютним кутом закручування. Утворюючі і на бічній поверхні циліндра переміщаються в положення 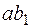і 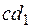відповідно, зміщаючись на кут зсуву .

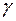Обчислимо довжину дуги 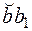(рис. 3.9 в), розглядаючи спочатку криволінійний трикутник аbb₁: 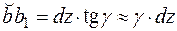, а потім трикутник

Оbb₁ : 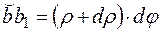(для малих кутів 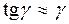). Зневажаючи нескінченно малими величинами другого порядку, одержуємо 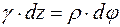, звідки .

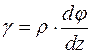Введемо поняття відносного кута закручування:

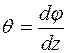, (3.6) тоді :

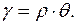(3.7)

Так як в нескінченно малому елементі виникає напружений стан чистого зсуву (рис. 3.9 г), то в межах малих деформацій виконується закон Гука при зсуві:

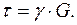(3.8)

З виразів (3.7) , (3.8) одержимо:

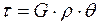. (3.9)

Остання залежність виражає закон Гука при крученні, на підставі якого можна зробити висновок про те, що дотичні напруження вздовж радіуса переріза змінюються по лінійному закону.

Підставимо залежність (3.9) у рівняння (3.5) та одержимо наступне:

,

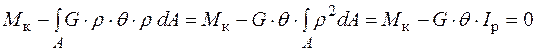де 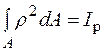– полярний момент інерції перерізу.

Це дає можливість визначити відносний кут закручування:

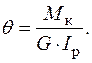(3.10)

Величина 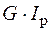називається жорсткістю вала при крученні.

З виразів (3.9), (3.10) одержуємо формулу для визначення дотичних напружень при крученні вала круглого чи кільцевого перерізів:

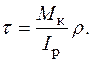(3.11) З рівняння (3.6) з урахуванням виразу (3.10) кут закручування дорівнює:

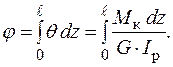
Якщо 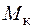, 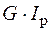є постійними величинами, то абсолютний кут закручування 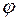вала можна обчислити за формулою:

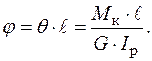(3.12)