ОБРАБОТКА РЕЗУЛЬТАТОВ ПРЯМЫХ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ

Смысл задачи обработки многократных (статистических) из­мерений состоит в том, чтобы получить оценку действительного значения измеряемой величины и определить погрешность этой оценки [1].

Способ обработки результатов статистических измерений за­висит от вида распределения. Наиболее хорошо отработаны ме­тоды обработки экспериментальных данных, если их распределение не противоречит нормальному закону. Однако для того, чтобы этими методами можно было воспользоваться, необходимо прежде доказать, что распределение опытных данных не противоречит нормальному закону. Главным фактором, затрудняющим идентификацию закона распределения, является всегда относительно малое количество экспериментальных данных. В этом случае следует максимально использовать априорную ин­формацию о виде распределения погрешностей. Эта информа­ция заключается в том, что кривая плотности распределения предполагается плавной и симметричной. Плавной кривая должна быть потому, что (в подавляющем большинстве случаев) сама измеряемая величина является непрерывной. Предположение о симметрии базируется на относительной малости размера по­грешности. Его также можно считать справедливым, так как в большинстве случаев, представляющих практический интерес, величина относительной погрешности измерений находится в интервале значений от долей, до нескольких единиц процента. Для того чтобы использовать вероятностно-статистические ме­тоды при обработке результатов многократных измерений, сис­тематические погрешности должны быть исключены (т. е. все ре­зультаты исправлены), либо должно быть заранее известно, что случайные погрешности много больше систематических. Прома­хи из совокупности опытных данных должны быть исключены экспериментатором.

Задача обработки прямых многократных измерений может формулироваться в двух вариантах:

1. Обработка результатов многократных измерений, когда за­ранее известно, что закон распределения опытных данных нор­мальный. Количество опытных данных в этом случае должно быть n ≥ 4. Обработка результатов в этом случае ведется по фор­мулам ГОСТ 8.207-76 Переиздание. Апрель 2006 г. «Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений. Основные положения» и результат представляется в виде формул по ПМГ 96-2009. «Государственная система обеспечения единства измерений. Результаты и характеристики качества измерений. Формы представления».

2. Обработка результатов многократных измерений, когда закон распределения заранее неизвестен. В этом случае вначале необходимо идентифицировать закон распределения опытных дан­ных, чтобы затем применить соответствующие вероятност­но-статистические методы обработки данных. Для уверенной идентификации закона распределения количество опытных дан­ных n должно удовлетворять условию 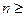50 (хотя эта граница достаточно условна).

Для того чтобы достаточно обоснованно выдвинуть гипотезу о виде закона распределения, экспериментальные данные груп­пируют и выборку представляют в виде гистограммы, состоящей из r столбцов с определенной протяженностью (h) соответствую­щих им интервалов. По виду полученной гистограммы и формулируется гипотеза о законе распределения опытных данных, ко­торую затем подтверждают с использованием соответствующего критерия согласия (либо отвергают и выдвигают новую, которую также необходимио затем подтвердить). При построении гистограм­мы следует соблюдать некоторые общие правила [2]. Опытные данные упорядочивают (представляют в виде ва­риационного ряда от X_min до Х_max в порядке возрастания) и группируют по интервалам. Ширину интервалов обычно выби­рают равной h:

h = (X_max - X_min)/r , (2.1)

где r - число интервалов разбиения.

Число интервалов разбиения нельзя выбирать очень большим или очень малым. При группировании данных в большое число мелких интервалов некоторые из них окажутся пустыми. Гисто­грамма будет иметь гребенчатый вид, т. е. резко отличаться от плавной кривой. Следовательно, если внутри гистограммы полу­чаются пустые интервалы, это чаще всего говорит о том, что число интервалов разбиения выбрано слишком большим.

При очень малом числе интервалов будут потеряны харак­терные особенности опытного распределения. Так, например, при трех интервалах любое колоколообразное распределение сведет­ся к треугольному. Задача оптимального выбора количества ин­тервалов не имеет в общем виде строгого решения. Для практи­ческих целей можно выбирать число интервалов r, руководству­ясь данными, приведенными ниже [3].

Количество наблюдений n в выборке 40 -100 100 -500 500 -1000

Число интервалов разбиения r 7-9 8 -12 10 -16

Предпочтительно выбирать число интервалов r нечетным, чтобы принудительно не уплощать островершинные распределения.

Значение ширины интервала h, определенное по форму­ле (2.1), нужно всегда округлять в большую сторону (например, h = 0,187 округляют до значения h = 0,2), причем желательно, чтобы h легко делилось на 2 (для определения координат цен­тров столбцов).

Нижняя граница первого интервала не обязательно должна быть равной X_min. Эта граница может быть выбрана несколько меньше значения X_min, но так, чтобы границы всех интервалов получались удобными для построения гистограммы (например, при X_min = 15,014 и h = 0,02 целесообразно выбрать Х_1н = 15,01, тогда Х_1в = 15,01+h = 15,03 и т. д.)

Масштаб по осям при построении гистограммы рекомендуется выбирать таким, чтобы высота графика относилась к его основа­нию как 3 к 5. При этом общая площадь между осью абсцисс и ступенчатой кривой должна быть равной единице (условие норми­ровки).

Следует заметить, что большинство перечисленных рекомен­даций соответствуют условиям, когда обработка результатов ста­тистических измерений проводится без применения компьютер­ных технологий. При использовании персональных компьюте­ров и соответствующих программных продуктов задача обработки результатов существенно упрощается.

Если из построенной гистограммы следует, что кривая опыт­ного распределения имеет форму, близкую к колоколообразной, целесообразно первой проверить гипотезу о нормальности рас­пределения опытных данных.

Алгоритм обработки результатов прямых многократных измерений при неизвестном законе распределения:

1. Упорядочиваем ряд наблюдений.

2. Находим оценку действительного значения измеряемой величины .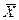

3. Находим оценку среднеквадратического отклонения для ряда наблюдений S_x.

4.Строим гистограмму опытного распределения и по виду гистограммы формулируем гипотезу о виде закона опытного рас­пределения. Как уже говорилось, при колоколообразной форме кривой опытного распределения первой проверяется гипотеза нормального распределения.

5. Используя критерий χ², проверяем состоятельность выдвинутой гипотезы (задача 2.1 – пример применения критерия χ² [1]).

Если гипотеза о нормальности распределения подтверждается, то дальнейшая обработка ведется по правилам, разработанным для нормально распределенных данных. Следующим шагом обработки является проверка выборки на наличие результа­тов, содержащих грубые погрешности, и исключение их.

Оконча­тельный результат представляется в форме по МИ 1317-2004 «Государственная система обеспечения единства измерений. Результаты и характеристики погрешности измерений. Формы представления. Способы использования при испытаниях образцов продукции и контроле их параметров».

6. Если по виду гистограммы выдвигалась гипотезао другом типе закона распределения (например, экспоненциальном, рав­номерном и др.) и она оказалась состоятельной, то оценки чи­словых характеристик опытного распределения и границы дове­рительного интервала случайной погрешности можно опреде­лить по формулам, приведенным в [3].

7. Если гипотеза о нормальности распределения опытных данных оказалась несостоятельной, а другие гипотезы не выдви­гались и не проверялись, то можно определить доверительный интервал случайной погрешности только при доверительной веро­ятности Р_дов = 0,9, пользуясь рекомендациями ГОСТ 11.001-73 и свойствами доверительного интервала при Р_дов = 0,9 (см. подразд. 1.2.2[1] и [2]) , при которой для большой группы различных распределений границы симметричного доверительного интервала определяются из соотношения .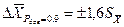

При этом следует иметь в виду, что по ограниченным экспери­ментальным данным мы получаем не точные доверительные значения, а лишь их приближенные значения - оценки. Достоверность оценок резко повышается с понижением значений Р_дов, а при постоянном Р_дов - с ростом числа отсчетов n. Поэтому оценки с большими доверительными вероятностями могут быть найдены только при большом числе отсчетов.

Располагая рядом из n отсчетов и отбрасывая с каждого из концов ряда по n_отб отсчетов, можно определить доверительный интервал D 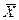_Рдов с доверительной вероятностью, не большей чем .

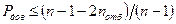Отсюда, число отсчетов n, необходимое для определения по экспе­риментальным данным D 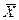_Рдов с заданной вероятностью Р_дов, будет не меньшим, чем 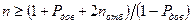и для различных значений Р_дов и n_отб=1 приведено ниже:

Р_дов 0,8 0,9 0,95 0,98 0,99 0,995 0,997

n 20 40 80 200 400 800 1333

По экспериментальным данным легко определить значение D 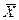лишь с доверительной вероятностью Р_дов ≤ 0,95 (n≈80), а определение D 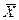_{Рдов=0,99} или D 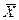_{Рдов=0,997} практически трудноосуществимо (нужно 400 ≤ n ≤ 1333). При этом необходимо обратить внимание на то, что, взяв, например, выборку объемом n = 80 и, отбросив с каждой стороны по одному отсчету, получим, что довери­тельная вероятность не может быть больше, чем 0,95. При этом нет никаких оснований утверждать, что она равна 0,95 (так же как утверждать, что она равна 0,8 или 0,3). Тем не менее, очень часто доверительные погрешности рассчиты­вают, вводя ничем не обоснованное предположение о том, что вид закона распределения погрешностей будто бы точно известен. В част­ности, используют прием, заключающийся в вычислении по небольшой выборке в 20-30 отсчетов оценки среднего квадратического отклоне­ния S 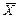, а затем указывают погрешность с доверительной вероятностью Р_дов = 0,997, равную D 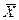_{Рдов=0,997} = 3σ на основании предположения о нормаль­ности закона распределения [2].

Например, согласно стандарту «ГОСТ 8.207-76. Переиздание. Апрель 2006 г.», если результаты наблюдений принадлежат нормальному распределению, а число результатов наблюдений n≤15, принадлежность их к нормальному распределению не проверяют, а доверительные границы результата измерения находят по формуле:

,

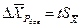где t – коэффициент Стьюдента.

Причем, коэффициент t находят по таблицам для доверительной вероятности Р_дов = 0,95. Как было показано выше, число наблюдений для доверительной вероятности 0,95 не должно быть меньше 80.

Из приведенного выше анализа ясно, что такой прием является некорректным вне зависимости от того, допускается ли он сознательно или неосознанно. Дело заключается в том, что реальные законы распределения погрешностей приборов весьма разнообразны и часто очень далеки от нормального. Для установления действительного хода кривой распределения на ее краях необходимо проведение испытаний, число которых должно быть тем больше, чем большим выбирается значение доверительной вероят­ности.

Все сказанное справедливо и при обработке результатов прямых многократных измерений при неизвестном законе распределения.

Если число измерений недостаточно велико, а доверительные границы результата измерения должны отвечать большой доверительной вероятности, за результат измерения лучше принять среднее арифметическое, а погрешность измерения рассчитывать по паспортным данным используемого средства измерения.

Задача № 2.1 [1]

Условие задачи.Для выяснения закона распределения слу­чайных отклонений изготовленных резисторов от номинала было проведено измерение точного значения 200 резисторов из одной партии. Номинальное значение резисторов 300 Ом. В ре­зультате предварительной обработки результатов измерений по­лучены следующие данные:

- максимальное значение резистора в выборке R_max = 308,97 Ом;

- минимальное значение резистора в выборке R_min = 287,05 Ом;

- среднее квадратическое значение отклонений резисторов от номинального значения S_DR = 5,146 Ом.

Примечание. Для экономии места вся совокупность полученных резуль­татов измерений резисторов здесь не приводится. В табл. 2 приведены сгруппированные по интервалам данные предварительной обработки откло­нений резисторов от номинала (столбцы 2—5 таблицы).

Решение.Для обоснованной формулировки гипотезы о виде закона распределения отклонений резисторов от номинала по­строим гистограмму опытного распределения, соблюдая все ре­комендации, приведенные в работах [2, 3, 4]. Для этого выпол­ним следующие действия.

1. Группируем полученные отклонения по интервалам, число которых выбираем r = 11.

2. Определяем ширину интервала, используя формулу (2.1):

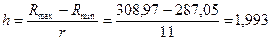Ом

или используя максимальные отклонения резисторов от номи­нала:

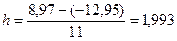Ом.