Обработка результатов обыкновенных косвенных измерений
Рассмотрим решение этой задачи для обыкновенных косвенных измерений, когда значения аргументов находятся путем прямых однократных измерений, корреляционная зависимость между погрешностями измеряемых аргументов отсутствует, а сами погрешности достаточно малы [3].
Уравнение измерений представляет собой явную нелинейную функцию двух аргументов (количество аргументов не меняет общего подхода к решению задачи): 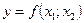 .
.
Оценки значений аргументов - 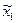 ;
; 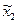 и абсолютные погрешности этих оценок -
и абсолютные погрешности этих оценок - 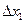 ;
; 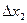 -известны. При этих условиях для решения задачи можно применить математический аппарат высшей математики, используемый для нахождения нового значения функции, которое она получает при малых приращениях аргументов.Как известно, новое значение функции может быть представлено рядом Тейлора:
-известны. При этих условиях для решения задачи можно применить математический аппарат высшей математики, используемый для нахождения нового значения функции, которое она получает при малых приращениях аргументов.Как известно, новое значение функции может быть представлено рядом Тейлора:

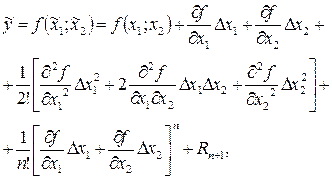 (3.4)
(3.4)
где 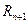 - остаточный член разложения функции в ряд.
- остаточный член разложения функции в ряд.
Для решения нашей задачи достаточно ограничиться линейным приближением, для чего в формуле (3.4) надо принять n= 1:
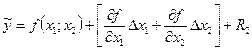 , (3.5)
, (3.5)
где 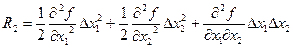 - остаточный член разложения.
- остаточный член разложения.
Величина остаточного члена может быть оценена при подстановке в 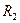 оценок аргументов
оценок аргументов 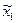 и
и 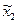 . Если при этом оказывается, что величина
. Если при этом оказывается, что величина 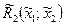 много меньше, чем
много меньше, чем 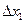 и
и 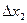 , то остаточным членом пренебрегают, т.е. используют линейное приближение разложения функции в ряд.По этой причине данный метод определения погрешности результата нелинейных косвенных измерений называют методом линеаризации. Таким образом, в этом случае оценка результата косвенного измерения может быть записана в виде:
, то остаточным членом пренебрегают, т.е. используют линейное приближение разложения функции в ряд.По этой причине данный метод определения погрешности результата нелинейных косвенных измерений называют методом линеаризации. Таким образом, в этом случае оценка результата косвенного измерения может быть записана в виде:
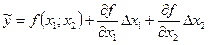 . (3.6)
. (3.6)
Используя (3.6), абсолютную погрешность косвенного измерения - 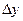 находим по общему правилу:
находим по общему правилу:
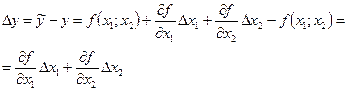 . (3.7)
. (3.7)
Распространяя полученное выражение на любое число аргументов, абсолютную погрешность нелинейного косвенного измерения можем записать:
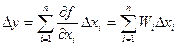 , (3.8)
, (3.8)
где 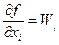 - частная производная от функции по
- частная производная от функции по 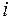 - му аргументу, вычисленная при подстановке в нее оценок аргументов
- му аргументу, вычисленная при подстановке в нее оценок аргументов 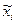 , называемая коэффициентом влияния (или функцией влияния) погрешности соответствующего аргумента на погрешность результата косвенного измерения;
, называемая коэффициентом влияния (или функцией влияния) погрешности соответствующего аргумента на погрешность результата косвенного измерения;
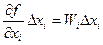 - частная абсолютная погрешность результата косвенного измерения от влияния погрешности i - го аргумента.
- частная абсолютная погрешность результата косвенного измерения от влияния погрешности i - го аргумента.
В зависимости от вида функции коэффициенты влияния для некоторых аргументов могут быть меньше единицы, а для некоторых из них - много больше единицы.
Выражение (3.8) с учетом (3.2) можно переписать в виде:
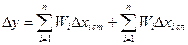 . (3.9)
. (3.9)
Как следует из (3.9) при определении погрешности результата косвенных измерений каждый раз приходиться решать задачу суммирования систематических и случайных погрешностей аргументов для определения соответствующей погрешности результата.
При этом сумма - 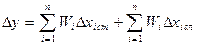 определяется с использованием формул (1.35 [1]) и, в зависимости от того, исправлялись ли результаты измерения каждого из аргументов (вводились ли поправки на систематические погрешности) или не исправлялись, равна либо систематической погрешности результата косвенного измерения, определенной при некоторой доверительной вероятности:
определяется с использованием формул (1.35 [1]) и, в зависимости от того, исправлялись ли результаты измерения каждого из аргументов (вводились ли поправки на систематические погрешности) или не исправлялись, равна либо систематической погрешности результата косвенного измерения, определенной при некоторой доверительной вероятности:
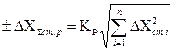 ,
,
если поправки не вводились, либо не исключённому остатку систематической погрешности результата косвенного измерения:
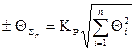 ,
,
если результаты измерений значений аргументов исправлялись.
Сумма - 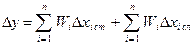 в (9), если случайные погрешности независимы и случайная погрешность каждого из аргументов оценена величиной СКП – Si, дает СКП результата косвенного измерения, определяемую с учетом (1.37 [1]) по формуле
в (9), если случайные погрешности независимы и случайная погрешность каждого из аргументов оценена величиной СКП – Si, дает СКП результата косвенного измерения, определяемую с учетом (1.37 [1]) по формуле
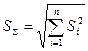 .
.
Границы доверительного интервала случайной погрешности результата косвенного измерения определяются в соответствии с (1.22 [1]).
Границы общей погрешности результата обыкновенных косвенных измерений определяют в соответствии с правилами, изложенными в разделе 1.3.1.[1] При этом в расчетных формулах под 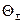 следует понимать не исключённый остаток систематической погрешности результата косвенного измерения -
следует понимать не исключённый остаток систематической погрешности результата косвенного измерения - 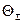 , а под СКП
, а под СКП 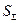 - СКП результата косвенного измерения -
- СКП результата косвенного измерения - 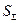 .
.
Важно учесть некоторые особенности метода определения погрешности результата косвенных измерений. В некоторых случаях нелинейная функция может иметь такой вид, что тот или иной аргумент фигурирует несколько раз и упрощению выражение не поддается. При вычислении коэффициентов влияния в этом случае необходимо после разложения в ряд Тейлора привести подобные по каждому аргументу члены. Приведение подобных членов следует выполнять, сохраняя те знаки, которые получились при дифференцировании исходной функции. И лишь тогда, когда получена окончательная формула, т. е. формула, в которую погрешность измерения каждого аргумента входит только 1 раз, можно переходить к численным расчетам и, смотря по условиям измерительной задачи, распоряжаться знаками перед слагаемыми.
Исходная формула (3.8), полученная для определения погрешности результата нелинейного косвенного измерения, пригодна только в том случае, когда погрешности аргументов выражены в абсолютной форме. Коэффициенты влияния 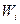 в этом случае являются размерными величинами и, после умножения на погрешность соответствующего аргумента, каждое произведение
в этом случае являются размерными величинами и, после умножения на погрешность соответствующего аргумента, каждое произведение 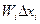 должно иметь размерность измеряемой ФВ у, что является хорошей проверкой правильности проводимых вычислений.
должно иметь размерность измеряемой ФВ у, что является хорошей проверкой правильности проводимых вычислений.
Иногда условиями измерительной задачи погрешности аргументов могут быть заданы в относительной форме, а переход к абсолютным значениям погрешностей невозможен, так как оценки значений аргументов неизвестны. В этом случае воспользоваться выражением (3.8) для оценки погрешности результата невозможно, и потребуется переход к относительной форме записи погрешности результата косвенного измерения.
Поэтому на практике предпочитают пользоваться уравнением относительной погрешности результата измерения[5].
Используя формулы (3.8) и (3.1), относительную погрешность результата можно записать в следующем виде [1]:
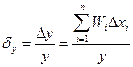 . (3.10)
. (3.10)
Разделив каждый член суммы на 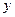 и преобразовав полученные выражения для ряда функций можно получить (3.10) в виде:
и преобразовав полученные выражения для ряда функций можно получить (3.10) в виде:
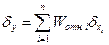 , (3.11)
, (3.11)
где 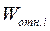 - коэффициент влияния для относительной погрешности измерений
- коэффициент влияния для относительной погрешности измерений 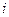 - го аргумента;
- го аргумента;
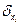 - относительная погрешность
- относительная погрешность 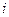 -го аргумента.
-го аргумента.
Коэффициенты влияния для относительных погрешностей - 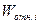 должны быть безразмерными величинами,что также является хорошей проверкой правильности проведенных преобразований в соответствии с (3.10).
должны быть безразмерными величинами,что также является хорошей проверкой правильности проведенных преобразований в соответствии с (3.10).
Отсюда следует, что для определения безразмерных коэффициентов влияния расчетно-аналитическим методом, необходимо:
1) получить аналитическое выражение функции (результат косвенного измерения) через значения аргументов 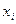 ;
;
2) взять частые производные функции по каждому из аргументов;
3) умножить полученные частные производные на отношение i-гo аргумента к значению функции;
4) подстановкой номинальных значений аргументов в выражения коэффициентов влияния, найти их численные величины.
Выполнение перечисленных операций, особенно нахождение частных производных, связано с большим количеством промежуточных преобразований и требует значительных затрат времени. Поэтому расчетно-аналитический метод, как правило, оказывается сложным и трудоемким даже при определении коэффициентов влияния аргументов на значение результата косвенного измерения, являющейся функцией 6-10 переменных.
Практика показывает, что в большинстве случаев аналитическое выражение результата косвенного измерения представляет собой дробную линейную, дробную рациональную или, реже, дробную иррациональную функцию параметров. Для названных видов аналитических выражений можно получить формулы для определения коэффициентов влияния, позволяющие полностью исключить промежуточные преобразования [5].
Рассмотрим случаи, когда аналитическое выражение результата косвенного измерения представляет собой дробную рациональную функцию параметров и, следовательно, записывается в виде:
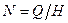 , (3.12)
, (3.12)
где 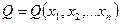 ,
, 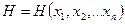 — многочлены, у которых показатель степени i-го параметра может быть больше единицы.
— многочлены, у которых показатель степени i-го параметра может быть больше единицы.
Из (3.12) по формуле (1.6) [5] найдем коэффициент влияния i-го параметра:
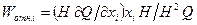 . (3.13)
. (3.13)
Предположим, что показатель степени параметра xi в числителе соотношения (3.12) равен m, в знаменателе – n.
Тогда, выполнив в (3.13) дифференцирование и необходимые элементарные преобразования, получим
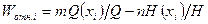 , (3.14)
, (3.14)
где Q(xi) и H(xi) – части многочлена Q и H, в которые входит аргумент xi.
Задача №3.1
Передаточное отношение кулисной передачи через радиус кривошипа l, расстояние между осями вращения кулисы и кривошипа c и угол поворота кривошипа 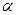 записывается в виде соотношения
записывается в виде соотношения
i = 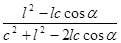 .
.
Требуется найти влияние радиуса кривошипа l и расстояния между осями c на величину передаточного отношения.
Выражения искомых коэффициентов влияния на основании (3.14) имеют вид:
Аi = 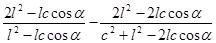 ;
;
Ac = 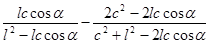 .
.
Дата добавления: 2020-10-14; просмотров: 715;











