Представление ряда Фурье в виде дискретных функций

Имея периодическую функцию: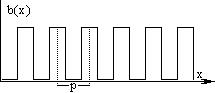

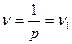
При чем 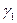- это первая гармоника. При преобразовании Фурье в пространственный дискретный ряд, мы нашу амплитуду выражаем дискретными значениями.

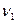Мы имеем первую или основную гармонику. При частоте мы уже можем отложить амплитуду первой гармоники:

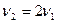
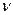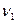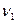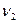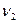Все гармоники отличаются в целое число раз. Между и - целое число, которое между и ; и 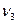всегда одинаково.

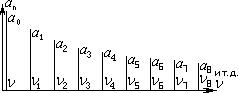
Ряд является бесконечным и меняется от 1 или 0 до 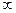. Но мы этот ряд можем ограничить числом членов, так как остальные пренебрежительно малы.

Бывает так, что отсутствуют либо четные, либо нечетные гармоники.

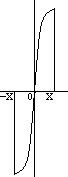
Если х и –х по модулю равны, то, то наша функция – четная – симметричная относительно оси х. Поэтому она теряет 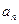-составляющую; т. е. cos-Фурье составляющие равны нулю; остаются только sin-Фурье составляющие.

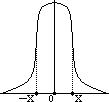
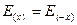
Если периодическая функция – нечетная – симметрична относительно оси у, то наш ряд теряет 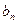-составляющую; т. е. cos sin -Фурье составляющие равны нулю; остаются только cos -Фурье составляющие.

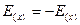
Ряды Фурье.

Обладают тем преимуществом, что он обладает наибольшей точностью при представлении функции, ограниченной числом членов. Ошибки являются минимальными. Другое преимущество – если мы эту функцию представляем разными членами ряда и их недостаточно; то мы добавляем число, но предыдущие члены ряда при добавлении не изменяются. И третье преимущество – это возможность упрощения ряда Фурье для четных функций.

Выше мы рассмотрели разложение функции в ряд Фурье. Это прямое преобразование ряда Фурье. Также мы можем получить обратное преобразование ряда Фурье.

Рассмотрим пример обратного Фурье-преобразования для прямоугольной решетки с п-образным распределением освещенности и с равной шириной штриха и просвета.

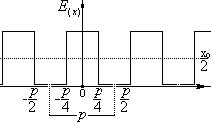
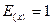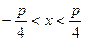
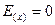при

при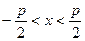

Мы можем записать ряд Фурье как:

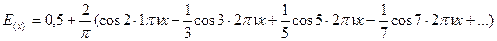
Представим теперь это графически. В нашей формуле 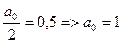. Следующий член – это первая или основная гармоника. Если у нас Р=0,1 мм, то у нас 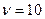мм. Четные гармоники у нас равны нулю. Следовательно, мы переходим сразу к третьей гармонике.

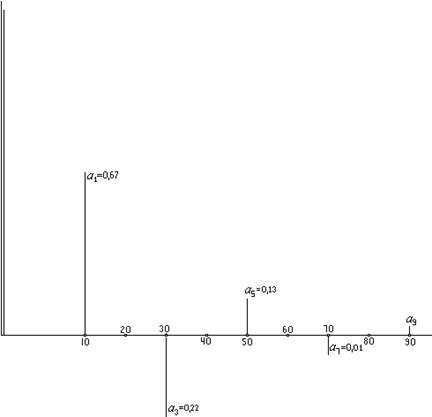
Мы ограничились пятью нечетными гармониками.. Сделаем обратное Фурье-преобразоование – найдем из наших гармоник функцию.

Берем нашу составляющую 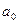и строим по ней амплитуду: . Откладываем 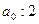и от нее откладываем гармонические составляющие синусоиды.

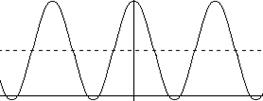1

Следующая гармоническая составляющая будет иметь амплитуду втрое меньшую, а частоту втрое большую.

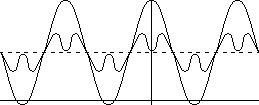1,2

Пятая гармоника будет иметь частоту в пять раз больше, а амплитуду в пять раз меньше.

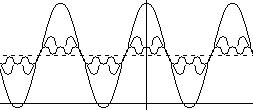1,2,3

Теперь суммируем наши гармоники.

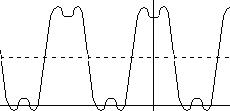1+2

Получаем уже достаточно приближенную к П-образному сигналу функцию. Чем больше членов ряда мы будем использовать, тем более точное у нас будет происходить обратное Фурье-преобразование.