Классификация штриховых изображений в зависимости от размеров (соотношения) деталей и ширины краевой функции(свойств изображения и свойств системы).
Исходя из длинны штриха, мы можем выделить четыре группы штриховых деталей, при учете, что краевая функция для всех этих групп одинаковая.
- Широкий штрих.
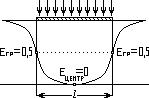
Для этого штриха характерно отсутствие пересечения краевых функций в центре штриха, вследствие чего освещенность в центре Емin =0; в том случае, если l – ширина зоны перехода краевой функции больше половины длинны штриха.
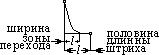
- Узкий штрих.
 L/2
L/2  lштриха
lштриха  L
L
Для этого штриха характерно то, что его две краевые функции пересекаются, но их окончания находятся внутри этого штриха. При суммировании этих двух функций мы получаем, что Е центра больше нуля, но меньше 0,5.
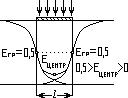
- Очень узкий штрих.
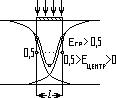
Здесь ширина такова, что когда мы строим краевые функции, то получаем, что они не только пересекаются, а и пересекают противоположную границу. Получаем, что Е пересечения границы функцией больше 0,5; но еще сохраняется, что Е центра больше нуля и все еще меньше 0,5.
- Супер узкий штрих.
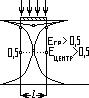
Здесь ширина такова, что Е пересечения границы функцией больше 0,5 и Е центра также больше 0,5.
Рассмотрим теперь классификацию такой детали как просвет – также в зависимости от размеров (соотношения) деталей и ширины краевой функции (свойств изображения и свойств системы). Однако, поскольку в данном случае мы рассматриваем не штрих, а просвет, то мы нормируем наше изображение единицей – используем формулу – Епросвета=Е1+Е2 – 1
Исходя из длинны просвета, мы можем также, как и со штрихом выделить четыре вида просвета, при учете, что краевая функция для всех этих групп одинаковая.
1. Широкий просвет.
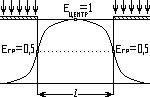
Для этого просвета характерно отсутствие пересечения краевых функций в его центре, вследствие чего освещенность в центре Емax =1; в том случае, если l – ширина зоны перехода краевой функции больше половины длинны штриха.
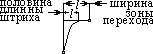
2. Узкий просвет.
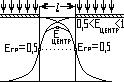 L/2
L/2 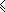 lштриха
lштриха  L
L
Для этого просвета характерно то, что его две краевые функции пересекаются, но их окончания находятся внутри этого просвета. При суммировании этих двух функций мы получаем, что Е центра уже меньше единицы, но больше 0,5.
3. Очень узкий просвет.
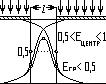
Здесь ширина такова, что когда мы строим краевые функции, то получаем, что они не только пересекаются, а и пересекают противоположную границу. Получаем, что Е пересечения границы функцией меньше 0,5; но еще сохраняется, что Е центра уже меньше единицы, но больше 0,5.
- Супер узкий просвет.
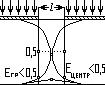
Здесь ширина такова, что Е пересечения границы функциями меньше 0,5 и Е центра также меньше 0,5.
Дата добавления: 2016-07-22; просмотров: 1621;











