Моделирование периодического штрихового изображения. Метод Фурье-преобразования. Пространственно-частотный анализ.
Очень часто в полиграфии мы имеем дело с периодическими решетками. Для этих периодических решеток можно использовать метод Фурье-преобразования.
Любая периодическая функция может быть разложена в ряд Фурье.
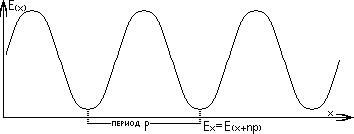
Эта функция может быть разложена в ряд: 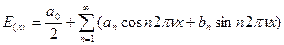
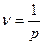 - это частота решетки, если мы рассматриваем пространственную решетку.
- это частота решетки, если мы рассматриваем пространственную решетку.
Обратное Фурье-преобразование: 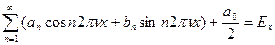
В данной формуле коэффициент 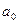 определяется как интеграл:
определяется как интеграл: 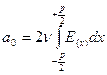
коэффициент 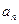 определяется как
определяется как 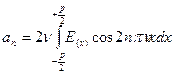
и коэффициент 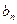 как
как 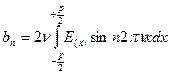 ; где
; где 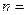 1, 2, 3, 4, …
1, 2, 3, 4, …
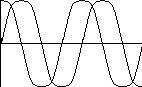
Учитывая, что разница между cos и sin только в 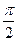 :
: 
И в векторной форме: 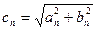
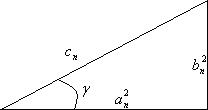
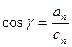 ,
, 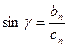 ;
; 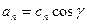 ,
, 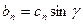 .
.
Подставляя сюда наше выражение:
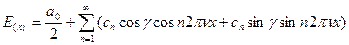
Мы знаем, что по формуле 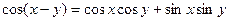
Отсюда получаем: 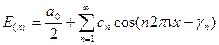
А также используя формулу Эйлера: 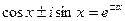
На основе формулы Эйлера мы можем записать нашу формулу:
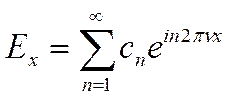
В этом выражении 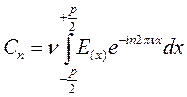
Таким образом мы совершили спектральный или гармонический анализ, в котором функция представлена в виде набора составляющих, отличающихся между собой по преобразованной частоте и амплитуде. Величины определяются по ним.
Сами гармонические составляющие отличаются между собой в целое число раз; причем каждая имеет свою амплитуду, отличающую 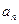 ,
, 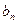 ,
, 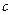 .
.
Дата добавления: 2016-07-22; просмотров: 1512;











