Возможности применения функции передачи модуляции для расчета воспроизведения в системе (четыре операции).

Функция передачи модуляции естественно пригодна в том случае, если мы имеем дело с периодическим изображением.

1. Расчет производится с периодическим изображением:

- анализ системы – это представление этого объекта в виде ряда Фурье. Графически можно представить в виде ряда Фурье:

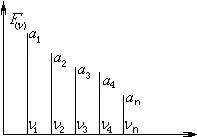
1. Находятся функции передачи модуляции системы – для этого существуют экспериментальные методы оценки ФПМ для отдельных систем или ряды систем прописать при помощи расчетных систем. Если система является сложной, состоящей из нескольких звеньев, то возможно нахождение отдельных звеньев и если эта система линейная, то перемножаются отдельные звенья ФПМ.

1. После нахождения ФПМ системы методом перемножения мы можем найти уже спектр изображения объекта в системе, для чего необходимо перемножить спектр изображения в системе 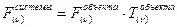. Нужно взять для каждой из гармоник спектра объекта соответствующее значение 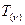и умножить 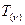соответственно на значение этих амплитуд.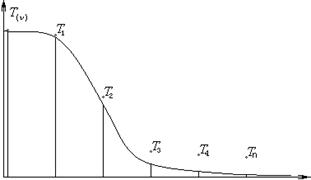
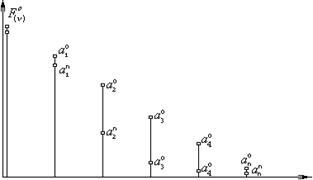
2. Осуществляем обратное Фурье-преобразование, суммируя эти гармонические составляющие.

Получаем очень урезанный спектр, при чем уже вторая гармоника будет очень урезана.

Если объект непериодический, то идея расчета остается той же самой, но сложнее; мы получаем сплошной спектр; второй этап такой же самый; мы находим ФПМ, затем производится обратное Фурье-преобразование.

Расчет для специальных

1. Находим ФПМ для отдельных звеньев системы.
2. Осуществляем расчет для ФПМ системы в целом методом каскадирования
3. Из этой ФПМ, которая классическая для синусоидального сигнала находим ФПМ для прямоугольного сигнала.
4. Из ФПМ для прямоугольного сигнала находим краевую функцию
5. Затем суммированием найденных краевых функций находим распределение который воспроизвелся в данной системе – штриховой объект.

Теорема о спектрах.

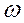-это круговая частота.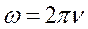

1. Пара преобразований Фурье

А) Прямое преобразование Фурье

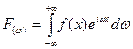
Б) Обратное преобразование Фурье

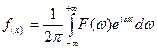
1. Соотношение масштаба функции и ее спектра

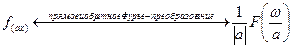Пример:

Возьмем функцию: 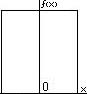Ее спектр будет: 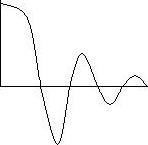по формуле: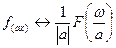

Если эта функция будет вдвое уже , то спектр ее будет вдвое шире: 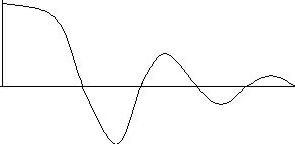По формуле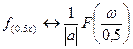

Если эта функция вдвое шире 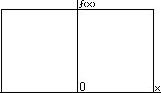, то ее спектр будет вдвое уже: 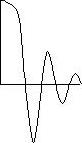По формуле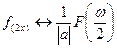

Если эта функция будет сведена к единичному импульсу, то ее спектр буде параллелен оси частот:

1. Принцип наложения или суперпозиций

Спектр суммы функций равен сумме спектров функции.

1. Теорема переноса или теорема запаздывания

Если у нас есть функция, которая смещается на 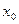, то у нас появляется фазовый сдвиг:

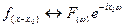
И обратно:

1. Если у нас есть функция, у которой спектр имеет сдвиг на 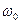, то сама функция будет изменена: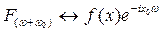

Функция сжимается и расширяется.

1. Теорема о спектре свертки

Если мы имеем свертку двух функций

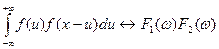при чем ;

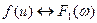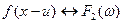
То Фурье-преобразование будет определяться произведением спектров.

Теорема о спектре произведения

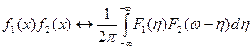
Спектр произведения функции равен свертке спектров этих функций.

Соотношение между спектром единичного, периодического и квазипериодического объектов.

1. Периодический объект

Периодический объект в виде прямоугольной решетки.

Этот объект характеризуется периодом p, шириной штриха и длинной штриха. Обычно длинна штриха и ширина просвета l равны друг другу.

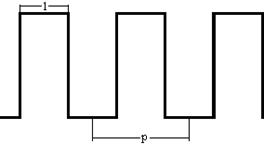
Выделим из этого объекта один единичный объект – штрих:

Для единичного объекта – спектр представляет собой функцию sinc:

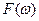=2 sinc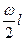

И спектр будет иметь вид:

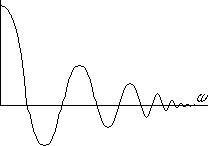
Частота будет равна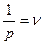

И мы получим из этого спектра выборку:

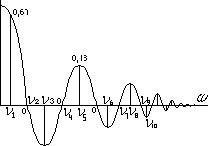
Для получения линейчатого спектра периодической решетки, нам надо осуществить выборку из спектра единичного объекта, формирующего эту решетку с частотой, соответствующей расстоянию между единичными объектами, формирующими эту решетку.

Квазипериодический объект – это отрезок периодического объекта на ограниченном пространстве. Из всего объекта выделяем кусок.

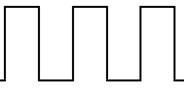
В результате получаем:

Наш спектр уже не истинно линейчатый, а вокруг каждой линии будет возникать спектр, определенный функцией sinc с параметром L.

Наш спектр будет иметь вид: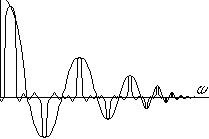

Чем уже кусок нашей решетки, тем шире будет расширение линии sinc.