Кинетика простой необратимой реакции
Рассмотрим простую необратимую реакцию типа:
A → R
протекающую при постоянном объеме реакционной смеси и постоянной температуре. Примем, что в начальный момент времени в исходной реакционной смеси присутствует только реагент и, значит, начальная концентрация продукта равна нулю. Эти условия запишем в виде:
T,V = const;
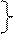 СА = САо при τ = 0
СА = САо при τ = 0
СR = СRо =0
Если объем реакционной смеси постоянный V = const, то скорость реакции это изменение концентрации в единицу времени:
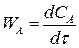 (2.5)
(2.5)
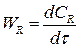 (2.6)
(2.6)
Теперь согласно уравнениям (2.2–2.4) составим кинетическую модель рассматриваемой реакции:
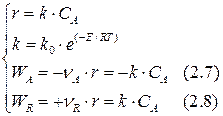
Сопоставим выражения (2.5) и (2.7), (2.6) и (2.8):
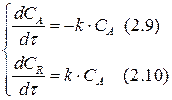
Определим изменение концентрации реагента А в ходе реакции. Для этого рассмотрим выражение (2.9). Разделим переменные, интегрируем его в пределах изменения концентрации от САо до СА и по времени от 0 до τ :
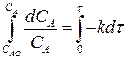
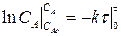
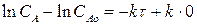
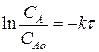
СА = САо е –кτ (2.11)
Выражение (2.11) представляет искомую зависимость изменения концентрации реагента А в ходе реакции или определяет вид кинетической зависимости СА = f(τ). Кинетическую зависимость СR = f(τ) найдем из материального баланса рассматриваемой реакции. Так как для нашей реакции νА = νR = 1, то САо =СА + СR. Тогда:
СR = САо - СА = САо - САо е–кτ = САо (1 – е–кτ ) (2.12)
Выражение (2.12) представляет искомую зависимость СR = f(τ).
Найдем зависимость степени превращения от времени для рассматриваемой реакции:
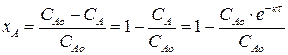
хА=1 – е–кτ (2.13)
Выражение (2.13) представляет искомую зависимость xА = f(τ).
Изобразим графически зависимости СА, СR, хА = f(τ).
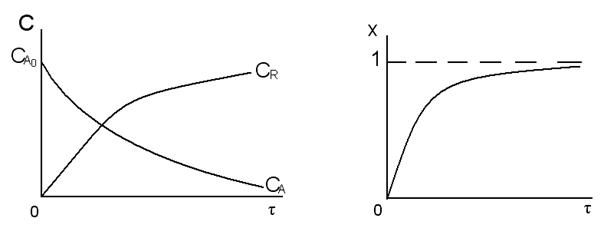
Из представленного следует, что для простой необратимой реакции, протекающей по схеме A→R, концентрация реагента А уменьшается в ходе реакции по экспоненциальной зависимости и стремится к нулю к концу реакции. Концентрация продукта R экспоненциально возрастает. Степень превращения реагента экспоненциально возрастает и стремится к единице.
Дата добавления: 2020-10-14; просмотров: 625;











