Раздел 1. Кинетическая модель обратимой реакции в общем виде

Рассмотрим обратимую гомогенную реакцию:

ν_АА + ν_ВВ € ν_RR + ν_SS

Скорость изменения количества любого j–го компонента W_j, участвующего в обратимой реакции, выражается соотношением:

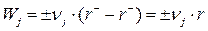
где ν_j – стехиометрический коэффициент при j–м компоненте («+» для продукта реакции, «–» для исходного вещества). Скорость обратимой реакции, определяемая по ЗДМ, равна разности скоростей прямой и обратимой реакций:

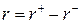
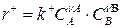– скорость прямой реакции,

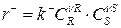– скорость обратной реакции.

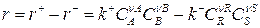
где E⁺, E^– – энергия активации прямой и обратной реакций; k⁺, k^– – константы скорости прямой и обратной реакций.

Тогда для обратимой реакции:

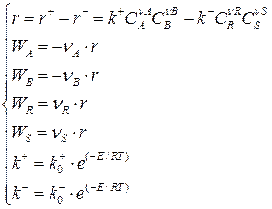(3.1)

Уравнения (3.1) образуют систему уравнений кинетической модели обратимой реакции.

Решим эту систему для гомогенной обратимой реакции типа А € R.

Раздел 2. Кинетика обратимой реакции А € R

Зададимся начальными условиями:

T,V = const;

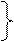С_А = С_Ао при τ = 0

С_R = С_Rо =0

Если V = const, то скорость реакции:

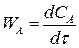(3.2)

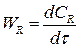(3.3)

Составим кинетическую модель рассматриваемой реакции:

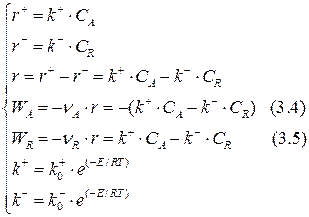
Сопоставим выражения (3.2) и (3.4), (3.3) и (3.5):

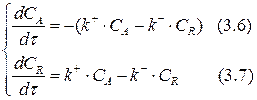
Определим изменение концентрации реагента А в ходе реакции.

Так как для нашей реакции ν_А= ν_R=1, то С_Ао = С_А + С_R. Тогда С_R = С_Ао – С_А. Подставим это выражение в уравнение (3.6):

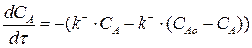
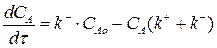(3.7)

В состоянии равновесия 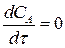и тогда выражение (3.7) примет вид:

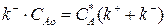(3.8)

где С^*_А – равновесная концентрация реагента А. Она является постоянной величиной для данной реакции при заданной температуре и давлении.

Подставим выражение (3.8) в (3.7):

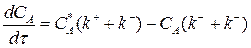
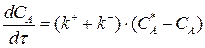
Разделим переменные, интегрируем от С_Ао до С_А и от 0 до τ :

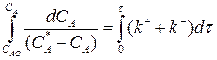
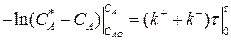
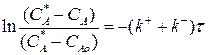
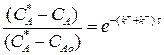
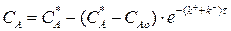(3.9)

Выражение (3.9) представляет искомую зависимость С_А = f(τ).

Изменение концентрации вещества R можно получить из уравнения материального баланса:

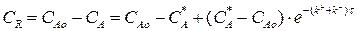(3.10)

Выражение (3.9) представляет искомую зависимость С_R = f(τ).

Получим зависимость степени превращения для данной обратимой реакции. Вспомним, что 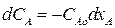. Тогда:

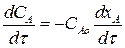(3.11)

Кроме того,известно, что 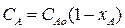. Тогда из материального баланса:

С_R = С_Ао – С_А = С_Ао – С_Ао(1– x_A) = С_Ао x_А (3.12)

Подставим выражения (3.11) и (3.12) в выражение (3.6):

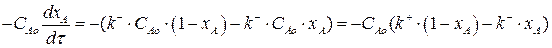
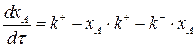
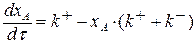(3.13)

В состоянии равновесия 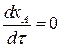. Тогда выражение (3.13) примет вид:

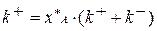(3.14)

где х_А^* – равновесная степень превращения вещества А. Это величина постоянная для данной реакции при заданной температуре и давлении.

Подставим выражение (3.14) в (3.13)

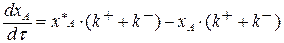
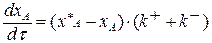
Разделим переменные, интегрируем от 0 до х_А и от 0 до τ :

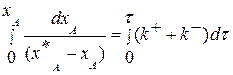
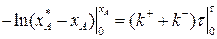
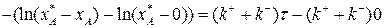
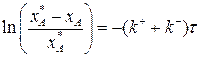
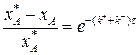
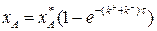(3.15)

Выражение (3.15) представляет искомую зависимость x_А = f(τ).

Изобразим графически зависимости С_А, С_R, х_А = f(τ) для обратимой реакции.

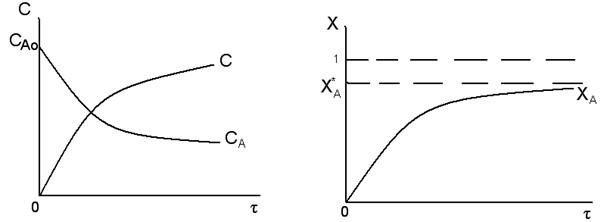Из представленного следует, что для рассматриваемой обратимой реакции, концентрация реагента А уменьшается в ходе реакции по экспоненциальной зависимости. Но в отличие от необратимой реакции концентрация реагента с течением времени стремится не к нулю, а к некому равновесному значению С_А^*, которое отлично от нуля. Концентрация продукта R экспоненциально возрастает, но в отличие от необратимой реакции не достигает большого значения, а стремится к некому равновесному значению С_R^*. Степень превращения реагента экспоненциально возрастает и стремится, в отличие от необратимой реакции к некой равновесной степени превращения х_А^*, которая всегда меньше единицы.