Яблонский А.А. Курс теоретической механики. Ч. 1, «Высшая школа», С-Птб.: 2002 и предшествующие издания.
Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах. Ч.1 и 2. М., 1961 и последующие издания
Контрольные задания для СРС – самостоятельно ответить на следующие вопросы: 1) Груз весом 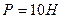 лежит на горизонтальной плоскости, статический коэффициент трения груза о плоскость
лежит на горизонтальной плоскости, статический коэффициент трения груза о плоскость 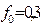 . Какая сила трения будет действовать на груз, когда к нему приложат горизонтальную силу Q , если: a)
. Какая сила трения будет действовать на груз, когда к нему приложат горизонтальную силу Q , если: a) 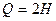 , б)
, б) 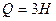 ? 2) Чем принципиально коэффициент трения качения отличается от коэффициента трения скольжения?
? 2) Чем принципиально коэффициент трения качения отличается от коэффициента трения скольжения?
Лекция 5. Кинематика точки
Цель лекции – изложить кинематику точки.
План лекции
1. Введение в кинематику
2. Основная задача кинематики. Кинематика точки
3. Способы задания движения точки
КРАТКОЕ СОДЕРЖАНИЕ ЛЕКЦИИ
Теоретическая механика определяется как наука о механическом движении. Тело движется, если оно с течением времени изменяет свое положение относительно некоторой системы отсчета. В этом определении подчеркивается, во-первых, относительность движения и, во-вторых, элемент времени; этим механическое движение отличается от простого перемещения, рассматриваемого в геометрии без учета времени.
Кинематика делится на кинематику точки и кинематику твердого тела. В кинематике время t принимается за независимую переменную, а все другие кинематические характеристики (перемещение, скорость, ускорение и т.п.) рассматриваются как функции времени.
Основной задачей кинематики является определение всех кинематических величин, характеризующих движение как отдельной точки, так и тела в целом. Эта задача может быть решена путем применения различных способов кинематического задания движения точки.
Векторный способ задания движения точки. Движение точки можно задать, если выразить ее радиус-вектор в некоторой системе отсчета в виде функции времени
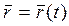 .
.
Функция 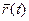 для определенности дальнейших рассуждений предполагается непрерывной, дважды дифференцируемой. Такое задание радиус-вектора точки предполагает наличие системы отсчета, но не конкретизирует ее. В данном случае траекторию точки можно определить как годограф ее радиус-вектора, т.е. геометрическое место концов радиус-вектора
для определенности дальнейших рассуждений предполагается непрерывной, дважды дифференцируемой. Такое задание радиус-вектора точки предполагает наличие системы отсчета, но не конкретизирует ее. В данном случае траекторию точки можно определить как годограф ее радиус-вектора, т.е. геометрическое место концов радиус-вектора 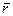 , изменяющегося во времени.
, изменяющегося во времени.
Скорость точки при векторном способе задания движения есть векторная величина, равная первой производной по времени от радиус-вектора точки; скорость всегда направлена по касательной к траектории в сторону движения точки, а ее численное значение определяется модулем 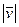 . Единица измерения скорости в СИ – м/с.
. Единица измерения скорости в СИ – м/с.
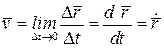
Ускорение точки по своему физическому смыслу есть изменение скорости, и определяется как первая производная по времени от скорости точки или как вторая производная от радиус-вектора точки; численное значение ускорения определяется модулем 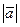 .
.
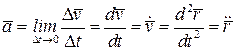
Единица измерения ускорения в СИ – м/c2.
Координатный способ задания движения точки. Чтобы знать положение точки в пространстве в любой момент времени необходимо иметь уравнения движения точки в виде:
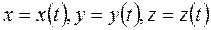 .
.
Эти выражения представляют собой уравнения движения точки в декартовой системе координат и одновременно являются уравнениями траектории точки, записанными в параметрической форме.
Чтобы найти уравнение траектории в форме непосредственной зависимости между координатами x,y,z, из уравнений движения необходимо исключить время.
В рассматриваемом случае скорость точки представляет собой сумму следующих векторов, параллельных осям декартовой системе координат:
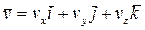 , где
, где 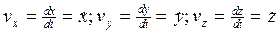 , а ее численное значение (модуль) определится по формуле
, а ее численное значение (модуль) определится по формуле
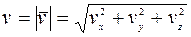
Формула для расчета ускорения примет вид
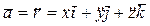 , где
, где 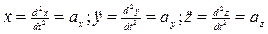 ,
,
а численное значение ускорения будет равно модулю вектора 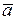 :
:
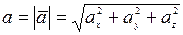
Естественный способ задания движения точки. Если траектория точки известна, только тогда можно применить естественный способ задания движения точки. Для этого необходимо: зафиксировать на траектории точку начало отсчета, выбрать положительное и отрицательное направления движения, задать закон движения точки по траектории в виде
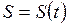 , где S- дуговая координата.
, где S- дуговая координата.
Всего этого в совокупности достаточно для однозначного определения положения точки в пространстве в любой момент времени.
Согласно определению скорости точки, учитывая определение единичного вектора 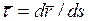 , получим:
, получим:
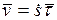 .
.
Отсюда следует, что проекция скорости точки на ось, касательную к траектории точки, равна
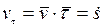 .
.
Эту производную иногда называют алгебраическим значением скорости точки.
Для ускорения точки имеем:
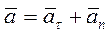 .
.
Проекции ускорения на оси естественной системы координат (касательную, нормаль и бинормаль) равны:
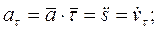
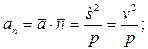
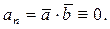
Очевидно, что 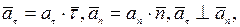 и модуль ускорения
и модуль ускорения
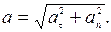
Характер движения точки по траектории можно определить исходя из знака произведения скорости и ускорения: в случае 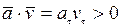 - движение точки ускоренное,
- движение точки ускоренное, 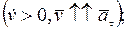 в случае
в случае 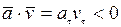 - движение точки замедленное
- движение точки замедленное 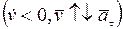 . При
. При 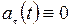 движение точки равномерное
движение точки равномерное 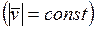 , в этом случае при движении по криволинейной траектории
, в этом случае при движении по криволинейной траектории 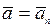 и
и 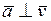 .
.
ГЛОССАРИЙ
| Теориялық механика | Теоретическая механика | Classical mechanics |
| Механикалық қозғалыс | Механическое движение | Mechanical motion |
| Материялық нүкте | Материальная точка | Particle |
| Санақ жүйе | Система отсчета | Frame of reference |
| Кинематика | Кинематика | Kinematics |
| Нүктенің траекториясы | Траектория точки | Trajectory of particle |
| Жылдамдық | Скорость | Velocity |
| Үдеу | Ускорение | Acceleration |
| Табиғи үш жақтың өстерi | Оси естественного трехгранника | Axes of a natural trihedral |
| Жанама үдеу | Касательное ускорение | Tangential acceleration |
| Нормаль үдеу | Нормальное ускорение | Normal acceleration |
Рекомендуемая литература
Дата добавления: 2016-07-22; просмотров: 3025;











