Яблонский А.А. Курс теоретической механики. Ч. 1 и 2, «Высшая школа», С-Птб.: 2002 и предшествующие издания.
М.И Бать, Г.Ю. Джанелидзе, А.С. Кельзон Теоретическая механика в примерах и задачах, 1 часть, Москва,1975 – 286-300с.
Контрольные задания для СРС – рассмотреть самостоятельно преобразование простейших движений (передаточные механизмы).
Лекция 7. Плоское движение твердого тела
Цель лекции – изложить теорию плоского движения твердого тела
План лекции
1. Теорема о скоростях точек плоской фигуры.
2. Теорема об ускорениях точек плоской фигуры.
КРАТКОЕ СОДЕРЖАНИЕ ЛЕКЦИИ
Плоским движением твердого тела называется такое движение, при котором каждая его точка движется в одной и той же плоскости, параллельной данной неподвижной плоскости.
Плоское движение часто встречается в технике. Большинство современных механизмов имеет звенья, совершающие плоские движения. Такие механизмы называются плоскими.
Уравнения
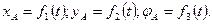 ,
,
определяющие положение и движение плоской фигуры в неподвижной плоскости Оxy, называются уравнениями плоского движения твердого тела.
Введем понятия алгебраической угловой скорости 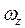 и алгебраического углового ускорения
и алгебраического углового ускорения 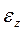 твердого тела в плоскопараллельном движении:
твердого тела в плоскопараллельном движении:
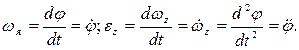
Для произвольного момента времени скорость точки твердого тела будет определяться следующей формулой:
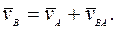
где 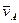 - скорость точки А , выбранной за полюс;
- скорость точки А , выбранной за полюс; 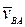 - скорость точки В тела при вращении ее вместе с фигурой вокруг полюса А. Вектор
- скорость точки В тела при вращении ее вместе с фигурой вокруг полюса А. Вектор 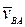 лежит в плоскости движущейся фигуры и
лежит в плоскости движущейся фигуры и 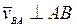 . Вектор
. Вектор 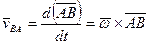 , его модуль:
, его модуль: 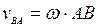 .
.
Окончательно имеем:
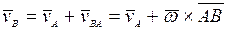 .
.
Таким образом, скорость какой-либо точки фигуры при ее плоском движении равна векторной сумме скорости полюса и скорости этой точки при ее вращении вместе с фигурой вокруг полюса.
Для определения ускорений точек плоской фигуры необходимо пользоваться следующей формулой:
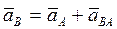
Здесь 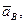
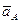 - ускорения точек В и А относительно неподвижной системы координат;
- ускорения точек В и А относительно неподвижной системы координат; 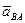 - ускорение точки В при ее вращательном движении вместе с плоской фигурой вокруг подвижной оси, проходящей через полюс А.
- ускорение точки В при ее вращательном движении вместе с плоской фигурой вокруг подвижной оси, проходящей через полюс А.
Таким образом, ускорение какой-либо точки плоской фигуры при плоском движении равно векторной сумме ускорения полюса и ускорения этой точки при ее вращательном движении вместе с плоской фигурой вокруг полюса.
Учитывая, что 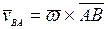 найдем:
найдем:
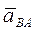
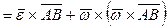 ,
,
где 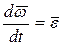 - угловое ускорение тела при плоском движении. Слагаемые вектора
- угловое ускорение тела при плоском движении. Слагаемые вектора 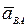 есть касательная и нормальная составляющие:
есть касательная и нормальная составляющие:
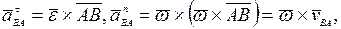
модули которых равны:
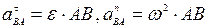 .
.
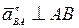 , вектор
, вектор 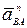 направлен от В к полюсу А..
направлен от В к полюсу А..
Таким образом,
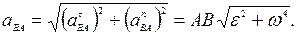
ГЛОССАРИЙ
| Қатты денеiң жазық-параллель қозғалысы | Плоско-параллельное движение твердого тела | Two-dimensional motion of rigid body |
| Лездiк жылдамдықтар центрi | Мгновенный центр скоростей | Instantaneous centre of zero-velocity |
| Лездiк үдеулер центрi | Мгновенный центр ускорений | Instantaneous centre of zero-acceleration |
| Қозғалмалы центроида | Подвижная центроида | Body cent rode |
| қозғалмайтын центроида | Неподвижная центроида | Space cent rode |
Рекомендуемая литература
Дата добавления: 2016-07-22; просмотров: 3030;











