Преобразование простейших движений твердого тела
Задание К2
4.2.1. Пример решения контрольного задания К2
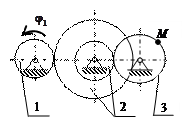
Рассмотрим пример решения задания для механизма, кинематическая схема которого приведена на рис. 4.2., где ведущим звеном является груз. Задано: закон изменения вертикальной координаты груза x(t) = 30 + 10t2, см; радиусы колес R1 = R3 = 10 см, R2 = 30 см, r2 = 20 см. Определить скорость и ускорение точки М для момента времени t1 = 1 c.
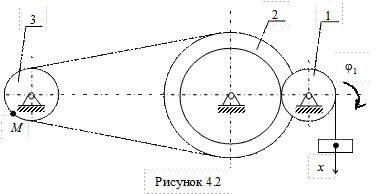
Решение
Обозначим и покажем на рис. 4.3 точки механизма А, В, D1, D2, через которые передается движение от одного звена (ведущего) к другому (ведомому).
Решение задачи начнем с определения скорости груза. Поскольку груз совершает поступательное движение, его можно считать точкой, движение которой задано координатным способом, и движется только вдоль оси x. Проекцию скорости груза на эту ось определим как производную от координаты x по времени
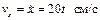 , при t1 = 1 с vx= 20 см/с.
, при t1 = 1 с vx= 20 см/с.
Поскольку знак проекции скорости груза на ось x положительный, вектор скорости направлен вниз, т.е. в положительном направлении оси x.
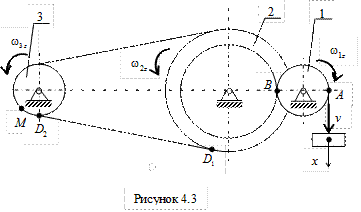
Скорости всех точек нити, на которой висит груз, одинаковы (нить считается нерастяжимой), скорость точки схода нити с барабана (колеса 1) равна скорости груза. Но точка А схода нити в данный момент времени принадлежит и колесу 1, совершающему вращательное движение вокруг неподвижной оси, что позволяет определить его угловую скорость. Направление угловой скорости колеса 1 соответствует направлению скорости точки А. Запишем теперь алгебраическое значение угловой скорости колеса 1
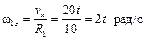 , при t1= 1с w1z= 2рад/с.
, при t1= 1с w1z= 2рад/с.
Колеса 1 и 2 находятся в зацеплении и имеют общую точку В (см. рис.4.3). Поэтому скорости точек колес, находящихся на их ободьях, одинаковы. При записи алгебраического значения угловой скорости колеса 2 учтем, что внешнее зацепление меняет направление вращения на противоположное
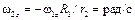 , при t1 = 1 с w2z = 1рад/с.
, при t1 = 1 с w2z = 1рад/с.
Одинаковы также скорости точек D1 и D2 , расположенных на шкивах ременной передачи. Однако здесь направление вращения не изменяется, поэтому
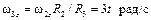 , при t1= 1 с
, при t1= 1 с 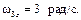
Определим теперь скорость точки M колеса 3 в момент времени t1 = 1 с. Величина скорости – это произведение модуля угловой скорости на расстояние от точки M до оси вращения, которое равно радиусу 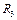 ,
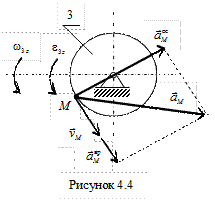
, 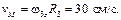 Направление вектора скорости покажем перпендикулярно радиусу, соединяющему точку с осью вращения, в соответствии с направлением вращения (рис. 4.4).
Направление вектора скорости покажем перпендикулярно радиусу, соединяющему точку с осью вращения, в соответствии с направлением вращения (рис. 4.4).
 Для нахождения ускорения точки M необходимо знать угловое ускорение колеса 3. Алгебраическое значение углового ускорения определим как производную по времени от алгебраического значения угловой скорости
Для нахождения ускорения точки M необходимо знать угловое ускорение колеса 3. Алгебраическое значение углового ускорения определим как производную по времени от алгебраического значения угловой скорости 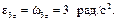 Алгебраические значения угловой скорости и углового ускорения имеют одинаковые знаки, следовательно, вращательное движение является ускоренным.
Алгебраические значения угловой скорости и углового ускорения имеют одинаковые знаки, следовательно, вращательное движение является ускоренным.
 Ускорение точки M определим как геометрическую сумму векторов вращательного и осестремительного ускорений, модули которых вычислим по формулам:
Ускорение точки M определим как геометрическую сумму векторов вращательного и осестремительного ускорений, модули которых вычислим по формулам:
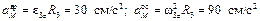 ,
,
откуда получим полное ускорение точки M
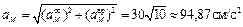 .
.
Векторы ускорений показаны на рис. 4.4. Движение колеса 3 ускоренное, поэтому вращательное ускорение точки M направлено в ту же сторону, что и ее скорость. Осестремительное ускорение всегда направлено к оси вращения.
Если в условии будет задан не закон движения груза x(t), а зависимость угла поворота колеса 1 от времени, например, j1(t) = 3+t 2, рад, изменения в решении задачи коснутся только начального этапа. Алгебраическое значение угловой скорости колеса 1 определим как производную от его угла поворота по времени 
Дальнейшее решение задачи не отличается от приведенного примера.
4.2.2. Условие и варианты задания К2
Задан закон движения ведущего звена механизма. В одних вариантах ведущим звеном является груз и задан закон изменения его вертикальной координаты x(t) в сантиметрах, а в других – одно из колес и задан закон изменения его угла поворота j(t)в радианах.Определить скорость и ускорение точки М для момента времени t1. Расчетные схемы задания К2 представлены табл. 4.3, а числовые исходные данные – в табл. 4.4.
Таблица 4.3
К2-1
| К2-2
|
К2-3
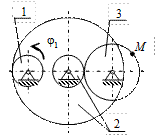
| К2-4
|
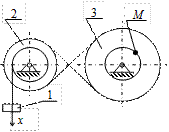
К2-5
| К2-6
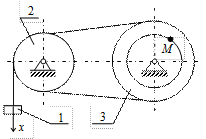
|
Продолжение табл. 4.3
К2-7
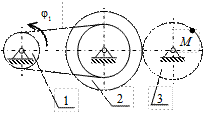
| К2-8
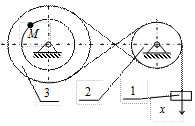
|
К2-9
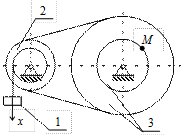
| К2-10
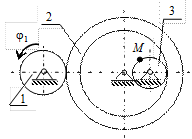
|
К2-11
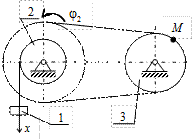
| К2-12
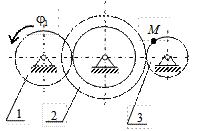
|
Продолжение табл. 4.3
К2-13
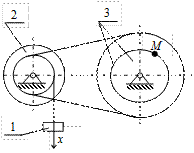
| К2-14
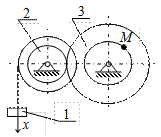
|
К2-15
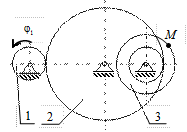
| К2-16
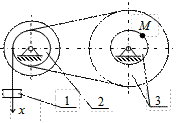
|
К2-17
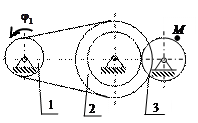
| К2-18
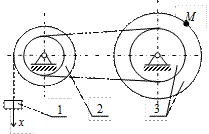
|
Продолжение табл. 4.3
К2-19
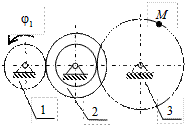
| К2-20
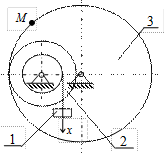
|
К2-21
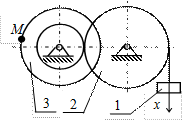
| К2-22
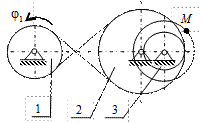
|
К2-23
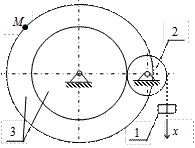
| К2-24
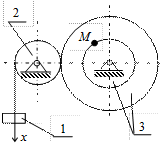
|
Таблица 4.4
| Номер варианта | Уравнение движения ведущего звена | R1, см | R2, см | r2, см | R3, см | r3, см | Момент времени, с |
| К2-1 | 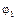 = 3+ t2 = 3+ t2
| – | 0,5 | ||||
| К2-2 | x=2+3t2 | – | |||||
| К2-3 | 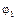 = 3+t2 = 3+t2
| – | |||||
| К2-4 | x= 4t2 | – | 0,5 | ||||
| К2-5 | 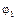 = 1+ t2 = 1+ t2
| – | 0,5 | ||||
| К2-6 | x= 4t2 | – | – | 0,5 | |||
| К2-7 | 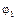 = 4+2t2 = 4+2t2
| – | |||||
| К2-8 | x= t2 | – | – | ||||
| К2-9 | x= 2t2 | – | |||||
| К2-10 | 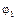 = 2 + 2t2 = 2 + 2t2
| – | 0,5 | ||||
| К2-11 | x= 5+ t2 | – | – | 0,5 | |||
| К2-12 | 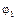 = t2 + 2 = t2 + 2
| – | |||||
| К2-13 | х= 3t2 + t | – | |||||
| К2-14 | x=10 + t2 | – | |||||
| К2-15 | 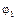 = 3 t2+ 2 = 3 t2+ 2
| – | |||||
| К2-16 | x=5t2 + 5 | – | |||||
| К2-17 | 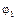 = 4t2 + 2 = 4t2 + 2
| – | |||||
| К2-18 | x= 6t2 | – | |||||
| К2-19 | 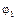 = 4t2 – 2 = 4t2 – 2
| – | |||||
| К2-20 | x=4 + t2 | – | – | ||||
| К2-21 | x=5t2 – 4 | – | – | ||||
| К2-22 | 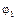 = 3 + 2t2 = 3 + 2t2
| – | |||||
| К2-23 | x= 4 + t2 | – | – | ||||
| x= 3 + t2 | – | – |
Дата добавления: 2020-10-14; просмотров: 657;











