ЗАДАНИЯ К КОНТРОЛЬНЫМ РАБОТАМ
Контрольные работы по кинематике включают три задания.
В задании К1 необходимо исследовать кинематику движения точки при координатном способе описания ее движения. В задании К2 необходимо определить кинематические характеристики преобразованных движений тел, а также скорости и ускорения их точек. В задании К3 необходимо определить кинематические характеристики твердого тела при плоскопараллельном движении, а также скорости и ускорения его точек. Для каждого контрольного задания в соответствующих таблицах приведено 24 варианта исходных данных, а для заданий К2 и К3 еще и 24 варианта расчетных схем.
Для выполнения контрольных работ необходимо:
1) внимательно прочитать соответствующий раздел в учебнике, выбранном из списка рекомендуемой литературы; ознакомиться с теоретическими сведениями и методическими рекомендациями настоящего пособия; составить краткий конспект, записав основные определения, теоремы и формулы;
2) ответить на контрольные вопросы;
3) разобрать решение типовых задач на примерах, приведенных в настоящем пособии;
4) самостоятельно выполнить индивидуальные контрольные задания в соответствии с предложенным преподавателем вариантом. Например, указан вариант К2-5, что означает следующее: К – раздел «Кинематика», 2 – номер темы раздела, 5 – номер варианта в задании К2;
5) оформить решенные задания в виде контрольной работы в отдельной тетради. Каждое выполненное задание должно содержать исходные данные и расчетную схему с указанием определяемых кинематических характеристик движения; решение должно быть изложено последовательно с краткими комментариями; в конце необходимо привести численные значения с размерностями определяемых величин;
6) зарегистрировать выполненные контрольные задания в установленные сроки в деканате заочного обучения у методиста.
Определение скорости и ускорения точки
По заданным уравнениям ее движения
Задание К1
4.1.1. Пример решения контрольного задания К1
Пусть точка М движется в плоскости xOy в соответствии с уравнениями
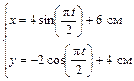 .
.
Для момента времени 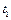 = 0,5 с найти положение точки М на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
= 0,5 с найти положение точки М на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
Решение
Заданный закон движения точки в координатной форме можно рассматривать как параметрические уравнения траектории точки. Исключим время t из уравнений движения и получим уравнение траектории точки в виде:
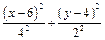 = 1.
= 1.
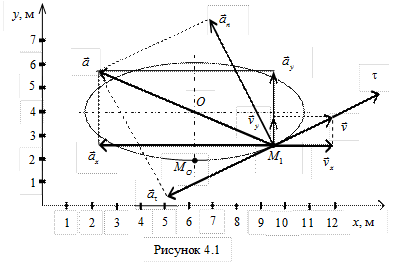
Таким образом, траекторией точки М является эллипс со смещенным центром, изображенный на рис. 4.1. Отметим на траектории положение точки М1 (x1, y1) в момент времени t1 = 0,5 c
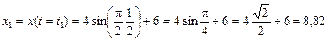 см;
см;
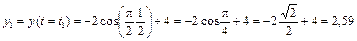 см.
см.
Вектор скорости точки представим в виде:
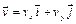 ,
,
где 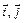 – орты координатных осей Оx и Оy;
– орты координатных осей Оx и Оy; 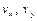 – проекции вектора скорости точки на координатные оси, которые равны 1-м производным от соответствующих координат по времени
– проекции вектора скорости точки на координатные оси, которые равны 1-м производным от соответствующих координат по времени
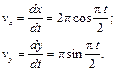
В момент времени t1 = 0,5 c
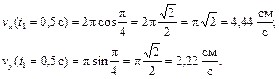
Вектор скорости точки 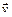 строим по двум взаимно перпендикулярным проекциям
строим по двум взаимно перпендикулярным проекциям 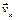 и
и 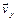 в соответствии с выбранным масштабом
в соответствии с выбранным масштабом
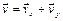 .
.
Полученный вектор должен быть направлен по касательной к траектории точки в сторону движения. Модуль скорости точки определим по уже найденным проекциям
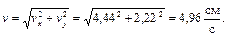
Вектор ускорения точки представим в виде:
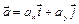 ,
,
где 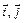 – орты координатных осей Оx и Оy;
– орты координатных осей Оx и Оy; 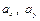 – проекции вектора скорости точки на координатные оси, которые равны 1-м производным от проекций вектора скорости или 2-м производным от соответствующих координат по времени:
– проекции вектора скорости точки на координатные оси, которые равны 1-м производным от проекций вектора скорости или 2-м производным от соответствующих координат по времени:
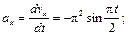

В момент времени t1 = 0,5 c
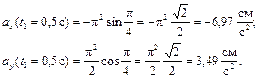
Вектор ускорения точки 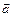 строим по двум взаимно перпендикулярным проекциям
строим по двум взаимно перпендикулярным проекциям  и
и 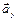 в соответствии с выбранным масштабом
в соответствии с выбранным масштабом
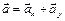 .
.
Полученный вектор ускорения точки в общем случае должен отклоняться от вектора скорости в сторону вогнутости траектории, а при движении по эллипсовидной траектории – проходить через центр эллипса. Модуль ускорения точки определим по уже найденным проекциям
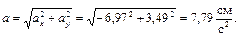
Вектор полного ускорения точки можно также представить в виде геометрической суммы его проекций на оси естественной системы отсчета
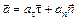 ,
,
где  и
и  – единичные орты касательной и главной нормали;
– единичные орты касательной и главной нормали; 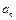 и
и 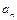 – соответственно проекции вектора ускорения на касательную и главную нормаль. Касательную М1t направляем по касательной к траектории в сторону движения точки движения, а главную нормаль М1n – перпендикулярно касательной в сторону вогнутости траектории. При вычислении касательного ускорения удобно воспользоваться формулой, устанавливающей связь между координатным и естественным способами задания движения точки
– соответственно проекции вектора ускорения на касательную и главную нормаль. Касательную М1t направляем по касательной к траектории в сторону движения точки движения, а главную нормаль М1n – перпендикулярно касательной в сторону вогнутости траектории. При вычислении касательного ускорения удобно воспользоваться формулой, устанавливающей связь между координатным и естественным способами задания движения точки
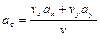 .
.
В момент времени t1 = 0,5 c
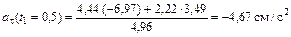 .
.
Значение касательного ускорения 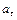 имеет отрицательный знак, следовательно, в данный момент времени движение точки замедленное и вектор касательного ускорения
имеет отрицательный знак, следовательно, в данный момент времени движение точки замедленное и вектор касательного ускорения 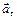 направлен в противоположную сторону направлению вектора скорости точки
направлен в противоположную сторону направлению вектора скорости точки 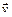 .
.
Нормальное ускорение 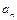 вычислим по формуле
вычислим по формуле  , если известен радиус кривизны траектории. Например, если точка движется по окружности радиусом R, то в любой точке траектории ρ = R. Если же траекторией движения точки является прямая, то
, если известен радиус кривизны траектории. Например, если точка движется по окружности радиусом R, то в любой точке траектории ρ = R. Если же траекторией движения точки является прямая, то 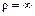 , следовательно,
, следовательно, 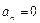 . В данном случае радиус кривизны траектории заранее не известен, поэтому нормальное ускорение определяем по формуле:
. В данном случае радиус кривизны траектории заранее не известен, поэтому нормальное ускорение определяем по формуле:
 .
.
В момент времени t1 = 0,5 c
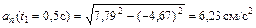 .
.
Построим векторы  и
и 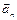 в соответствии с уже выбранным масштабом, а затем сложим их геометрически. В результате получим тот же вектор полного ускорения точки
в соответствии с уже выбранным масштабом, а затем сложим их геометрически. В результате получим тот же вектор полного ускорения точки 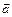 , который ранее уже был получен геометрической суммой составляющих
, который ранее уже был получен геометрической суммой составляющих 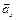 и
и 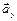 . Этот факт служит контролем правильности решения.
. Этот факт служит контролем правильности решения.
Радиус кривизны траектории в рассматриваемой точке определим по формуле
 .
.
В момент времени t1 = 0,5 c
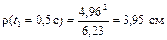 .
.
Результаты всех вычислений для заданного момента времени приведены в табл. 4.1.
Таблица 4.1
| Координаты, см | Скорости, см/с | Ускорения, 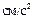
| ρ, см | |||||||
| x | y | 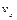
| 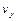
| 
| 
| 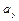
| 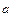
| 
| 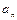
| |
| 8,82 | 2,59 | 4,44 | 2,22 | 4,96 | –6,97 | 3,49 | 7,79 | –4,67 | 6,23 | 3,95 |
Примечание. В последнем столбце через ρ обозначен радиус кривизны траектории в точке 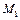 .
.
4.1.2. Условие и варианты задания К1
По заданным уравнениям движения точки М установить вид ее траектории и для момента времени 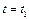 найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
Исходные данные для решения приведены в табл. 4.2.
Таблица 4.2
| Номер варианта | Уравнения движения | Время
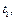 с с
| |
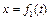 , см , см
|  , см , см
| ||
| К1-1 | 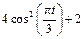
| 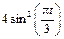
| |
| К1-2 | 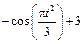
| 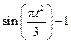
| |
| К1-3 | 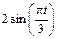
| 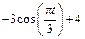
| |
| К1-4 | 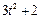
| –4t | 0,5 |
| К1-5 | 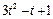
| 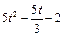
| |
| К1-6 | 
| 
| |
| К1-7 | 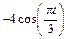
| 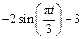
| |
| К1-8 | 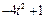
| –3t | 0,5 |
| К1-9 | 
| 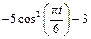
| |
| К1-10 | 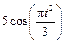
| 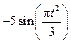
| |
| К1-11 | 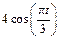
| 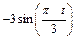
| |
| К1-12 | 3t | 4t2 + 1 | 0,5 |
Продолжение табл. 4.2 
| Номер варианта | Уравнения движения | Время
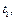 с с
| |
| К1-13 | 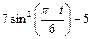
| 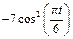
| |
| К1-14 | 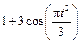
| 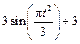
| |
| К1-15 | –5t2 – 4 | 3t | |
| К1-16 | 2 – 3t – 6t2 | 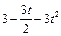
| |
| К1-17 | 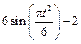
| 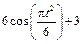
| |
| К1-18 | 7t2 – 3 | 5t | 0,25 |
| К1-19 | 3 – 3t2 + t | 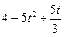
| |
| К1-20 | 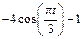
| 
| |
| К1-21 | –6t | 2t2 – 4 | |
| К1-22 | 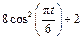
| 
| |
| К1-23 | 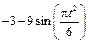
| 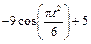
| |
| К1-24 | –4t2 + 1 | –3t |
Дата добавления: 2020-10-14; просмотров: 632;











