Мгновенный центр скоростей

Простой и наглядный способ определения скоростей плоской фигуры основан на понятии о мгновенном центре скоростей (МЦС). Им называют точку подвижной плоскости, в которой расположена плоская фигура S и скорость которой в данный момент времени равна нулю.

Доказана теорема о том, что если тело движется не поступательно, то такая точка существует, и притом единственная. Из определения следует, что в общем случае в каждый момент времени МЦС находится в различных точках плоскости. При вращательном движении тела вокруг неподвижной оси, являющимся частным случаем плоскопараллельного движения, МЦС в любой момент времени расположен на оси вращения. Если же тело движется поступательно или мгновенно поступательно (скорости всех точек тела в данный момент времени равны по величине и совпадают по направлению), то МЦС находится на бесконечно большом расстоянии от любой точки тела. Выбрав в качестве полюса точку Р, которая является в данный момент времени МЦС, а значит 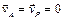, из формулы (3.4) для определения скорости любой точки плоской фигуры найдем скорость точки М

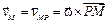. (3.8)

Следовательно, скорость любой точки тела в данный момент времени находим так же, как при вращении вокруг неподвижной оси, проходящей через МЦС и перпендикулярной плоскости движения. Таким образом, при плоскопараллельном движении скорость любой точки тела перпендикулярна отрезку, соединяющему эту точку с МЦС, а модуль скорости пропорционален расстоянию до МЦС

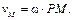(3.9)

Угловая скорость плоской фигуры равна отношению скорости какой-либо ее точки к расстоянию от этой точки до МЦС

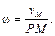(3.10)

Способы определения положения мгновенного центра скоростей:

1) если известны направления скоросте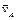й и 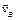точек А и В плоской фигуры, то МЦС (точку Р) определяют как точку пересечения перпендикуляров к скоростям 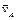и 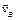, проведенных из этих точек (рис. 3.3,а);

2) если скорости двух точек тела A и B известны по модулю, параллельны друг другу ( 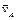|| 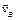), и перпендикулярны прямой AB, то МЦС находят в точке пересечения прямой АВ с прямой, соединяющей концы векторов скоросте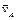й и 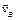(рис. 3.3,б,в);

3) при качении без скольжения одного тела по неподвижной поверхности МЦС находят в точке соприкосновения тел (рис. 3.3,г), так как при отсутствии скольжения скорость этой точки подвижного тела равна нулю;

4) если скорости точек A и B тела 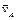и 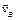параллельны друг другу ( 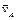|| 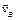) и не перпендикулярны прямой АВ, то перпендикуляры к ним также параллельны друг другу. В этом случае МЦС находится в бесконечном удалении от точек A и B, движение тела является мгновенно поступательным, следовательно, скорости всех точек тела равны, а его угловая скорость в данный момент времени равна нулю.

С помощью МЦС плоскопараллельное движение можно представить не только как сложное, состоящее из поступательного и вращательного движений, но и как простое движение, состоящее из серии элементарных последовательных поворотов вокруг МЦС. Необходимо отметить, что положение МЦС в пространстве во все время движения меняется. Геометрическое место точек МЦС подвижного тела называют подвижной центроидой, а неподвижного тела – неподвижной центроидой. Таким образом, плоскопараллельное движение представляет собой качение без скольжения подвижной центроиды по неподвижной центроиде.

Пример 1. Колесо катится без скольжения по неподвижной прямой поверхности. Скорость точки O постоянна и равна 100 см/с (рис. 3.4,а).

Определить угловую скорость колеса, скорости точек A, B, C и ускорения точек A, C, P, если R = 50 см, r = 40 см.

Решение

Колесо совершает плоскопараллельное движение. Качение происходит без скольжения, следовательно, в данном случае точка касания колеса с неподвижной поверхностью – точка P – является МЦС. Определим угловую скорость колеса согласно формуле (3.10)

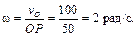
Зная расстояния от точек A, B и C до МЦС, можно найти их скорости по формуле (3.9)

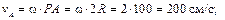
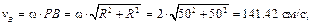
Векторы скоростей точек колеса направлены перпендикулярно отрезкам, соединяющим их с МЦС (см. рис. 3.4,б). В соответствии с теоремой о проекциях скоростей двух точек тела на прямую, соединяющую эти точки, убеждаемся в правильности полученных результатов.

Перейдем к определению ускорений, для чего воспользуемся формулами (3.6) и (3.7). В качестве полюса выбираем точку O. Ускорение полюса равно нулю, так как эта точка движется равномерно и прямолинейно. Поэтому ускорения точек будут равны их ускорениям во вращательном движении вокруг полюса. Например, для точки А

.

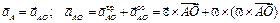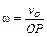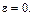Дифференцируя по времени выражение и учитывая, что OP = const и = const, получим Таким образом, ускорения всех точек, включая МЦС, состоят из осестремительных ускорений во вращении вокруг полюса О

;

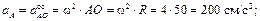
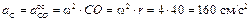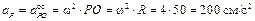
и направлены от соответствующих точек к полюсу (см. рис 3.4,в).

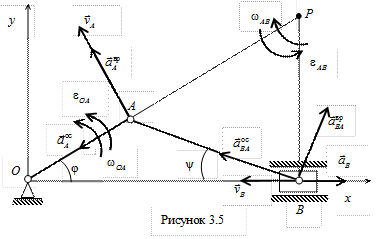
Пример 2. Кривошип ОА кривошипно-ползунного механизма, приведенного на рис. 3.5, вращается вокруг неподвижной оси с угловой скоростью 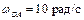и угловым ускорением 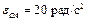. Положение механизма определяется углом .

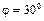Найти угловую скорость и угловое ускорение шатуна АВ, а также скорость и ускорение ползуна B, если длина кривошипа ОА = 10 см, а длина шатуна АВ = 30 см.

Решение

Вначале определим скорость точки А кривошипа

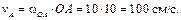
Затем, зная направления скоростей точек А и В, найдем положение МЦС на пересечении перпендикуляров к скоростям этих точек – точку P. Для определения угловой скорости шатуна и скорости точки В находим длины отрезков, соединяющих точки А и В с МЦС. Из теоремы синусов следует, что

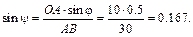
Вычислим длины отрезков:

.

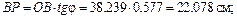
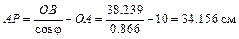Теперь найдем искомые величины:

Определим ускорение точки В и угловое ускорение шатуна АВ. Здесь надо иметь в виду, что расстояние от точки А до МЦС не является постоянным и зависит от положения механизма, т.е. от времени. Поэтому продифференцировать по времени угловую скорость шатуна не представляется возможным. Поступим следующим образом. Для нахождения ускорения точки В воспользуемся векторным равенством (3.6)

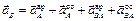
и спроецируем его на оси координат xOy (см. рис. 3.5). При этом учтем, что вектор 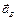лежит на прямой ОВ, так как точка В движется прямолинейно, вектор 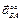направлен к полюсу А, а вектор 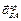перпендикулярен ему. Получим два алгебраических уравнения для определения величин и направлений ускорени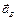й и 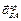(вначале направляем искомые векторы произвольно):

;

.

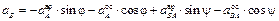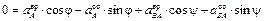Предварительно вычислим составляющие ускорения согласно формулам (3.7):

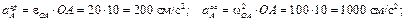
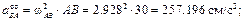
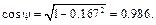
Далее определим:

– из 2-го уравнения

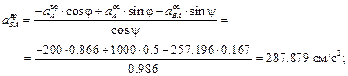
– из 1-го уравнения

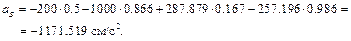
Знаки показывают, что направление ускорения 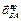совпадает с принятым, а направление 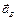– противоположно направлению, указанному на рис. 3.5. Зная ускорение 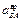, можно найти угловое ускорение шатуна

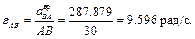
Вопросы для самоконтроля

1. Какое движение твердого тела называют плоскопараллельным?

2. На какие простейшие движения можно разложить плоскопараллельное движение?

3. Какие уравнения описывают плоскопараллельное движение?

4. Как определяют скорость произвольной точки плоской фигуры, если известна скорость полюса?

5. Какую точку плоской фигуры называют мгновенным центром скоростей (МЦС)?

6. Как распределены скорости точек тела по отношению к МЦС?

7. Какие существуют способы определения положения МЦС?

8. Как определяют ускорения произвольных точек тела, совершающего плоскопараллельное движение?