Преобразования простейших движений твердого тела

В различных механизмах часто осуществляют преобразование простейших движений: поступательное – во вращательное, вращательное – в поступательное, а также передачу вращательного движения от одного элемента механизма к другому.

Рассмотрим определение угловой скорости барабана 2 при заданной скорости груза 1, подвешенного на тросе, намотанном на барабан (рис. 2.2). Скорости всех точек троса, на котором подвешен груз, одинаковы (трос считают нерастяжимым), скорость точки схода троса с барабана колеса равна скорости груза. Но с этой точкой соприкасается точка, принадлежащая колесу, которое совершает вращательное движение, и имеющая ту же скорость, что позволяет определить угловую скорость колеса. При этом будем полагать, что положительному движению груза соответствует положительное вращение колеса.

Запишем алгебраическое значение угловой скорости 2-го колеса

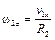. (2.18)

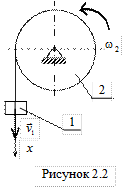
Аналогично можно определить скорость груза по заданной угловой скорости колеса

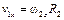. (2.19)

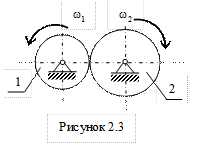
При передаче вращения от одного элемента к другому используют зубчатые или фрикционные зацепления (рис. 2.3, 2.4), а также цепные или ременные передачи (рис. 2.5, 2.6). В случае зубчатого зацепления колеса 1 и 2 имеют общую точку, поэтому скорости точек, находящихся на их ободьях, одинаковы, т.е.

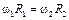. (2.20)

При записи алгебраического значения угловой скорости 2-го колеса учтем, что внешнее зацепление (см. рис. 2.3) меняет направление вращения на противоположное:

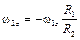, (2.21)

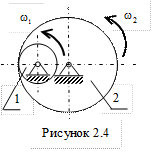
а внутреннее зацепление (см. рис. 2.4) его не меняет

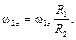(2.22)

	Рисунок 2.5

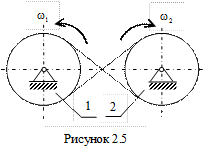
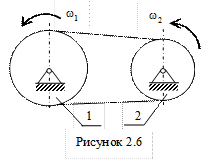
Одинаковы модули скоростей и для соответствующих точек на шкивах ременной передачи (имеются в виду те точки, где ремень, который считается нерастяжимым, сходит с одного шкива и наматывается на другой). Направление вращения может также либо изменяться на противоположное при передаче движения (см. рис. 2.5), либо не изменяться (см. рис. 2.6). Угловую скорость при этом определяют соответственно по формулам (2.16) и (2.17).

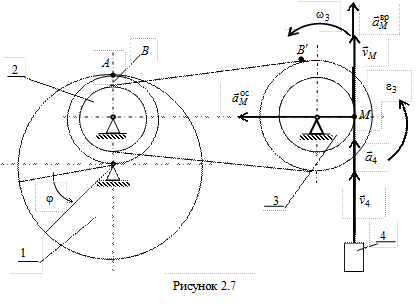
Пример. Колесо 1 (рис. 2.7) вращается вокруг неподвижной оси по закону j = 2t²+4, рад и приводит в движение механизм подъёма груза 4. Механизм состоит из двух ступенчатых колес 2 и 3, соединенных ременной передачей и вращающихся вокруг неподвижных осей.

Определить скорость и ускорение груза 4 в момент времени t = = 3 с, если R₁ = 40 см, R₂ = 15 см, R₃ = 25 см, r₂ = 10 см, r₃ = 20 см.

Решение

Определим угловую скорость зубчатого колеса 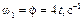. Точка контакта колес 1 и 2 является в данный момент времени их общей и ее скорость 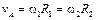, откуда 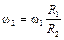. Далее, приравнивая скорости точек B и 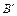, принадлежащих в этот момент времени колесам 2, 3, получим связь между угловыми скоростями этих колес ,

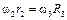откуда 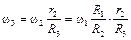. Подставляя выражение для угловой скорости 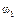и значения радиусов колес, определим

.

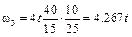Так как 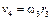, вычислим скорости точки М и груза 4 при t = 3 с

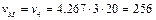см/с.

Ускорение груза 4 равно вращательному ускорению точки М, т.е.

.

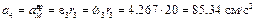Вопросы для самоконтроля

1. Что называют степенями свободы твердого тела?

2. Сколько степеней свободы имеет твердое тело в общем случае его движения в пространстве?

3. Какие виды движения твердого тела называют простейшими?

4. Каковы основные свойства поступательного движения твердого тела?

5. Какое движение твердого тела называют вращением вокруг неподвижной оси?

6. Каковы основные кинематические характеристики движения тела, вращающегося вокруг неподвижной оси?

7. Как связаны между собой угол поворота тела, угловая скорость и угловое ускорение при вращении его вокруг неподвижной оси?

8. Как направлены векторы угловой скорости и углового ускорения при вращении тела вокруг неподвижной оси?

9. Как определяют скорости точек тела, вращающегося вокруг неподвижной оси?

10. Как определяют ускорения точек тела, вращающегося вокруг неподвижной оси?