Множественная корреляция

До сих пор мы рассматривали корреляционные связи между двумя признаками: результативным (у) и фактор­ным (х). Например, выпуск продукции зависит не только от размера основного капитала, но и от уровня квалифи­кации рабочих, состояния оборудования, обеспеченности и качества сырья и материалов, организации труда и т.д. В связи с этим возникает необходимость в изучении, из­мерении связи между результативным признаком, двумя и более факторными. Этим занимается множественная корреляция.

Множественная корреляция решает три задачи. Она определяет:

1) форму связи;

2) тесноту связи;

3) влияние отдельных факторов на общий результат.

Определение формы свя­зи сводится обычно к отысканию уравнения связи у с фак­торами x,z,w,...у. Так, линейное уравнение зависимости результативного признака от двух факторных определяет­ся по формуле

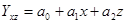(8.28)

Для определения параметров а₀, а_} и а₂, по способу наименьших квадратов необходимо решить следующую систему трех нормальных уравнений:

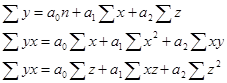(8.29.)

При определении тесноты связи для множественной зависимости пользуются коэф­фициентом множественной (совокупной) корреляции, предварительно исчислив коэффициенты парной корреля­ции. Так, при изучении связи между результативным признаком у и двумя факторными признаками — х и z, нужно предварительно определить тесноту связи между у и х, между у и z, т.е. вычислить коэффициенты парной кор­реляции, а затем для определения тесноты связи резуль­тативного признака от двух факторных исчислить коэф­фициент множественной корреляции по следующей фор­муле:

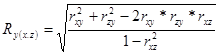(8.30.)

где r_xy, r_zy, r_xz — парные коэффициенты корреляции.

Коэффициент множественной корреляции колеблется в пределах от 0 до 1. Чем он ближе к 1, тем в большей мере учтены факторы, определяющие конечный резуль­тат.

Если коэффициент множественной корреляции возве­сти в квадрат, то получим совокупный коэффициент де­терминации, который характеризует долю вариации резуль­тативного признака у под воздействием всех изучаемых факторных признаков.

Совокупный коэффициент детерминации, как и при парной корреляции, можно исчислить по следующей фор­муле:

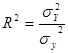(8.31)

где 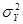— дисперсия факторных признаков, 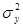— диспер­сия результативного признака. Однако вычисление теоретических значений Y при множественной корреляции и сложно, и громоздко. Поэтому факторную дисперсию 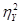исчисляют по следующей формуле:

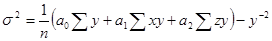(8.32)

Проверка существенности связи при множественной корреляции, по сути, ничем не отличается от проверки при парной корреляции.

Поскольку факторные признаки действуют не изоли­рованно, а во взаимосвязи, то может возникнуть задача определения тесноты связи между результативным при­знаком и одним из факторных при постоянных значениях прочих факторов. Она решается при помощи частных ко­эффициентов корреляции. Например, при линейной связи частный коэффициент корреляции между х и у при по­стоянном z рассчитывается по следующей формуле:

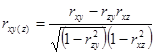(8.33)

В настоящее время на практике широкое распростра­нение получил многофакторный корреляционный анализ.