Элементы прогнозирования и интерполяции
Применение прогнозирования предполагает, что закономерность развития, действующая в прошлом (внутри ряда динамики), сохранится и в прогнозируемом будущем, т.е. прогноз основан на экстраполяции. Экстраполяция, проводимая в будущем называется перспективной и в прошлое – ретроспективной.
Теоретической основой распространения тенденции на будущее является инерционность, которая позволяет выявить сложившиеся взаимосвязи, как между уровнями динамического ряда, так и между группой связанных рядов динамики. На основе рядов динамики получаются весьма надежные прогнозы, если уровни ряда динамики сопоставимы и получены на основе единой методологии.
Экстраполяцию в общем виде можно представить формулой:
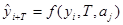 (9.29.)
(9.29.)
где 
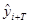 - прогнозируемый уровень
- прогнозируемый уровень
yi – текущий уровень прогнозируемого ряда
T – Период упреждения
aj – параметр уравнения тренда.
В зависимости от тог, какие принципы и исходные данные положены в основу прогноза, выделяют следующие элементарные методы экстраполяции: среднего абсолютного прироста, среднего темпа роста и экстраполяцию на основе выравнивания рядов по какой – либо аналитической формуле.
· Прогнозирование по среднему абсолютному приросту
Для нахождения интересующего нас аналитического выражения тенденции на любую дату t необходимо определить средний абсолютный прирост и последовательно прибавить его к последнему уровню ряда столько раз, на сколько периодов экстраполируется ряд.
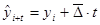 (9.30.)
(9.30.)
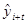 - экстаполируемый уровень: (i+t) – номер этого уровня (года),
- экстаполируемый уровень: (i+t) – номер этого уровня (года),
i – номер последнего уровня (года) исследуемого периода, за который рассчитан 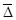 ,
,
t – срок прогноза период упреждения,
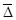 -средний абсолютный прирост.
-средний абсолютный прирост.
Однако следует иметь в виду, что использование среднего абсолютного прироста для прогноза возможно только при следующем условии:
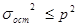
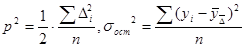 (9.31.)
(9.31.)
· Прогнозирование по среднему темпу прироста
Осуществляется в случае, когда есть основание считать, что общая тенденция ряда характеризуется показательной (экспоненциальной) кривой. Для нахождения тенденции необходимо определить средний коэффициент роста, возведенный в степень, соответствующую периоду экстраполяции, т.е. по формуле:
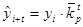 (9.32.)
(9.32.)
yi - последний уровень ряда динамики,
t – срок прогноза,
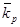 - средний коэффициент роста.
- средний коэффициент роста.
· Прогнозирование на основе аналитического выравнивания тренда
При этом для выхода за границы исследуемого периода достаточно продолжить значения независимой переменной времени (t).
При таком подходе к прогнозированию предполагается, что размер уровня, характеризующее явление, формируется под воздействием множества факторов, причем не представляется возможным выделить отдельно их влияние. В связи с этим ход развития связывается не с какими–либо конкретными факторами, а с течением времени, т.е. y = f(t). При анализе рядов динамики иногда приходится прибегать к определению некоторых неизвестных уровней внутри данного ряда динамики, т.е. интерполяции.
Интерполяция может проводится на основе абсолютного прироста, среднего темпа роста и с помощью аналитического выравнивания. Она так же основана на том или ином предположении тенденции изменения уровней, характер этого прогноза несколько иной: здесь уже не приходится предполагать, что тенденция, характерная для прошлого сохранится и в будущем.
Вопросы для теоретического контроля знаний:
1. Для чего нужно изучать динамику явлений?
2. Дайте определение ряда динамики. Из каких элементов он состоит и каков их смысл?
3. Какие существуют виды рядов динамики?
4. Какие динамические ряды называются моментными и почему их уровни нельзя суммировать?
5. Какие ряды статистических величин называются интервальными? Почему их уровни можно суммировать? Приведите примеры.
6. Каковы причины возникновения несопоставимости динамических рядов?
7. Какие приемы применяются для преобразования несопоставимых рядов динамики в сопоставимые?
8. Как исчисляется средняя для интервального ряда? Приведите примеры.
9. Как исчисляется средняя для моментного ряда? Приведите примеры.
10. Что характеризуют показатели абсолютного прироста и как они исчисляются?
11. Что представляет собой темп роста? Как он исчисляется?
12. Какая существует взаимосвязь между последовательными цепными коэффициентами роста и базисным коэффициентом роста за соответствующий период? Каково практическое применение этой взаимосвязи?
13. Чему равен средний абсолютный прирост?
14. По какой формуле исчисляется средний темп роста?
15. Как исчисляется средний темп прироста?
16. Какими наиболее распространенными статистическими методами осуществляется изучение тренда в рядах динамики?
17. В чем сущность метода укрупнения интервалов и для чего он применяется?
18. Как производится сглаживание рядов динамики способом скользящей (подвижной) средней? В чем достоинства и недостатки этого метода?
19. В чем сущность метода аналитического выравнивания динамических рядов?
20. Как определяется тип уравнения тенденции динамики?
21. Охарактеризуйте технику выравнивания ряда динамики по прямой.
22. Что представляют собой сезонные колебания, в чем практическое значение их изучения?
23. Как исчисляются индексы сезонности?
24. Что такое экстраполяция и интерполяция рядов динамики?
Примеры решения задач:
1. Требуется провести анализ динамики продажи мясных консервов за 1997 –2001 г.г. Для удобства и наглядности исходные и рассчитанные показатели изложены в табличной форме (табл. 9.1.)
Таблица 9.1.
Динамика продажи мясных консервов в одном из регионов за 1999 – 2003гг. и расчет аналитических показателей динамики (данные условные).
| Годы | Консервы мясные, млн. усл. банок | Абсолютные приросты (снижение), млн. усл. банок | Темпы роста, % | Темпы прироста, % | Абсолютное значение 1% прироста , млн. усл. банок | |||
| с предыдущим годом | с 1997 г. | с предыдущим годом | с 1997г. | с предыдущим годам | с 1997г. | |||
| А | ||||||||
| - | - | - | 100,0 | - | 0,0 | - | ||
| -85 | -85 | 90,5 | 90,5 | -9,5 | -9,5 | 8,91 | ||
| +789 | +704 | 197,9 | 179,0 | 97,9 | 79,0 | 8,06 | ||
| +42 | +746 | 102,63 | 183,7 | 2,63 | 83,7 | 15,95 | ||
| +14 | +760 | 100,85 | 185,3 | 0,85 | 85,3 | -16,37 | ||
| Итого | +780 | - | - | - | - | - | - |
Абсолютный прирост: 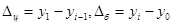
В нашем примере абсолютное уменьшение продажи консервов за 2000г. по сравнению с 1999г. составило: 806 – 891 = - 85 млн. усл. банок (табл. 9.1., гр.2), а по сравнению с базисным 1999г. продажа консервов возросла в 2003г. на 760 млн. усл. банок (гр.3).
Темп роста: 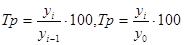
Для 2003г. темп роста по сравнению с 1999г. составил 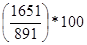 = 185,3 % (табл. 9.1., гр. 5).
= 185,3 % (табл. 9.1., гр. 5).
Темп прироста: 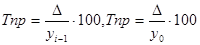
Показывает, например, на сколько процентов продажа консервов в 2003г. возросла по сравнению с 1997г.: 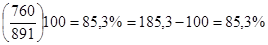 (гр. 6,7).
(гр. 6,7).
Показатель абсолютного значения одного процента прироста: 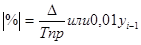 ;
;
Для 2003г. абсолютное значение 1% прироста равно: 0,01*16,37 = 16,37 или 14: 0,0855 = 16,37 млн. банок.
Среднегодовой абсолютный прирост( 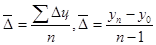 ) продажи мясных консервов за 1999 – 2003гг. равен
) продажи мясных консервов за 1999 – 2003гг. равен 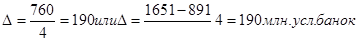
Среднегодовой темп роста ( 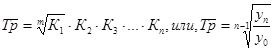 )продажи мясных консервов за 1999 – 2003гг. рассчитаем двумя способами:
)продажи мясных консервов за 1999 – 2003гг. рассчитаем двумя способами:
Тр = 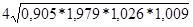 =
= 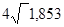 = 1,167 или 116,7%;
= 1,167 или 116,7%;
Тр = 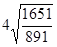 =
= 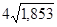 =1,167 или116,7%.
=1,167 или116,7%.
Среднегодовой темп прироста ( 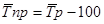 )получим, вычтя из среднего темпа роста 100%.
)получим, вычтя из среднего темпа роста 100%.
Тпр = 116,7% - 100% = 16,7%
2. Выявить сезонные колебания по следующим данным о числе разводов по месяцам за 1995 – 1997 гг.
| Месяцы | Число расторгнутых браков | Индекс сезонности | |||
| в среднем за три года | |||||
| Январь | 165,7 | 122,4 | |||
| Февраль | 147,0 | 108,6 | |||
| Март | 150,7 | 111,3 | |||
| Апрель | 136,0 | 100,4 | |||
| май | 136,0 | 100,4 | |||
| Июнь | 125,7 | 92,8 | |||
| Июль | 126,0 | 93,1 | |||
| Август | 120,7 | 89,1 | |||
| Сентябрь | 118,0 | 87,2 | |||
| Октябрь | 128,0 | 94,5 | |||
| Ноябрь | 131,7 | 97,3 | |||
| Декабрь | 139,3 | 102,9 | |||
| Средний уровень ряда | 138,7 | 135,6 | 131,8 | 135,4 | 100,00 |
1. Произведем осреднение уровней одноименных периодов:
уянв. 95 + у янв. 96 + у янв. 97195+158+144
январь = 3 = 3 = 165,7;
у дек.95 + удек. 96 + у дек. 97138+141+139
декабрь = 3 = 3 = 139,3.
2. По месячным средним уровням определим средний общий уровень
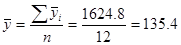

3. По месяцам определим индексы сезонности
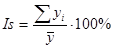
Iянв. = (165,7 : 135,4) 8 100% = 122,4%
Iдек. = ( 147,0: 135,4) * 100% = 108,6%.
3. На основе данных о производстве стиральных машин произвести сглаживание методом трехчленной средней.
| Месяцы | Стиральные машины, тыс. шт. | Трехчленные скользящие суммы | Трехчленные скользящие средние |
| - | - | ||
| - | 161,7 | ||
| 153,7 | |||
| 152,0 | |||
| 145,3 | |||
| 145,0 | |||
| 140,7 | |||
| 134,3 | |||
| 137,7 | |||
| 142,3 | |||
| 153,00 | |||
| 155,3 |
Взяв данные за первые три месяца исчисляем трехчленные суммы, а затем средние:
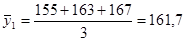
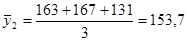 и т.д.
и т.д.
4. С помощью метода аналитического выравнивания по прямой выразите основную тенденцию по следующим данным о производстве молока:
| Годы | млнн. т., у | t | t2 | ty | y-i | y - y-i | (y - y-I)2 |
| 13,3 | -2 | -26,6 | 13,02 | 0,28 | 0,08 | ||
| 13,5 | -1 | -13,5 | 13,94 | -0,44 | 0,19 | ||
| 14,8 | 14,86 | -0,0 | 0,00 | ||||
| 16,1 | 16,1 | 15,78 | -0,32 | 0,10 | |||
| 16,6 | 33,2 | 16,70 | -0,1 | 0,01 | |||
| Итого | 74,3 | - | 9,2 | 74,30 | - | 0,38 |
Уровни ряда динамики выражаются в виде функции времени: 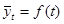
Для выравнивания ряда динамики по прямой используем уравнение: 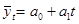
Способ наименьших квадратов дает систему уравнений для нахождения параметров а0 и а1.
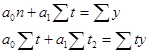
y – исходный уровень ряда;
n – число членов ряда;
t – показатель времени, который обозначается порядковыми номерами, начиная с низшего, например,
| годы | |||||
| t |
Решение системы уравнений позволяет получить выражения для параметров а0 и а1:
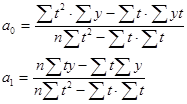
Но техника может быть упрощена. Тогда уравнения примут следующий вид: 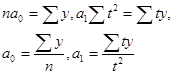
Расчеты необходимых значений представлены в таблице.
а0 = 74,3 : 5 = 14,86; а1 ==9,2 : 10 = 0.92.
В результате получаем следующее уравнение основной тенденции производства молока в регионе за 1993 – 1997 г.г.: 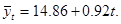
Подставляя в уравнение принятые обозначения t, вычислим выровненные уровни ряда динамики:
1993: у-1 = 14,86 +0,92 (-2) = 13,02;
1994: у-2 = 14,86 + 0,92 (-1) = 13,94 и т.д.
Задания для самостоятельной работы:
1.Имеются следующие данные о производстве продуктов животноводства:
| Годы | Мясо, млн. т | Молоко, млн. т. |
| 10,0 | 72,6 | |
| 12,3 | 83,6 | |
| 15,0 | 90,8 | |
| 13,6 | 89,7 | |
| 14,7 | 94,9 | |
| 15,3 | 94,5 | |
| 15,5 | 93,3 | |
| 15,1 | 90,9 | |
| 15,2 | 88,9 | |
| 15,3 | 90,1 |
По каждому виду продукции рассчитайте среднегодовые абсолютные приросты, среднегодовые темпы роста и прироста.
2..По следующим данным о производстве молока в РФ за 1990-1995 гг., млн.т:
1990 1991 1992 1993 1994 1995
13,3 13,5 14,8 16,1 16,6 16,4
Определите среднегодовые абсолютные приросты, среднегодовые темпы роста, среднегодовые темпы прироста.
3.Используя взаимосвязь показателей динамики, определите уровни ряда динамики и недостающие в таблице цепные показатели динамики по следующим данным о производстве продукции предприятиями (в сопоставимых ценах):
| Годы | Производство продукции, млн. руб. | По сравнению с предыдущим годом | ||
| абсолютный прирост, млн. руб. | темп роста, % | темп прироста, % | ||
| 92,5 | ||||
| 4,8 | ||||
| 104,0 | ||||
| 5,8 | ||||
| 7,4 | ||||
| 7,0 |
4. Имеются следующие данные о внутригодовой динамике поставки шерстяных тканей в розничную сеть области по кварталам за 1995 – 1997 гг., млн. руб.:
| Кварталы | |||
| 171,9 | 160,0 | 172,1 | |
| 132,8 | 113,1 | 176,8 | |
| 144,4 | 124,2 | 139,1 | |
| 154,7 | 155,8 | 141,2 |
Для анализа внутригодовой динамики продажи шерстяных тканей: а) определите индексы сезонности; б) изобразите графически сезонную волну развития изучаемого явления по месяцам года. Сделайте выводы.
Литература:
1.Елисеева И.И., Юзбашев М.М. Общая теория статистики, М.: Финансы и статистика, 1996.- с.257 –267.
2.Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики. М.: Инфра – М, 2000. –с.281-338.
3.Гусаров В.М. Статистика. М.: ЮНИТА – ДАНА, 2001. –с.106-141.
4.Общая теория статистики под ред.Спирина А.А. М.: Финансы и статистика, 1996.-с.155-206.
5.Статистика: курс лекций под ред. Ионина В.Г. Изд – во НГАЭИУ, М.: Инфра – М, 1997. –с.91-111.
6. Теория статистики под ред. Шмойловой Р.А. М.: Финансы и статистика, 2002. – с.334 -398.
Дата добавления: 2016-07-22; просмотров: 4314;











