Измерение тесноты связи

Чтобы измерить тесноту прямолинейной связи между двумя признаками, пользуются парным коэффициентом корреляции, который обозначается r

Так как при корреляционной связи имеют дело не с приращением функции в связи с изменением аргумента, а с сопряженной вариацией результативных и факторных признаков, то определение тесноты связи, по существу, сводится к изучению этой сопряженности, т.е. того, в ка­кой мере отклонение от среднего уровня одного признака сопряжено с отклонением другого. Это значит, что при наличии полной прямой связи все значения (х —X) и (у — Y) должны иметь одинаковые знаки, при полной обратной — разные, при частичной связи знаки в преобладающем чис­ле случаев будут совпадать, а при отсутствии связи — совпадать примерно в равном числе случаев.

Для оценки существенности коэффициента корреляции пользуются специально разработанной таблицей критичес­ких значений г.

Коэффициент корреляции r_xy. применяется только в тех случаях, когда между явлениями существует прямолиней­ная связь.

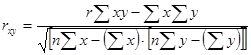(8.16.)

Если же связь криволинейная, то пользуются индексом корреляции, который рассчитывается по форму­ле:

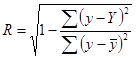
(8.17)

где у — первоначальные значения; 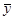— среднее значение; Y— теоретические (выравненные) значения переменной величины.

Показатель остаточной, случайной дисперсии опреде­ляется по формуле:

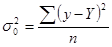
(8.18)

Она характеризует размер отклонений эмпирических значений результативного признака y от теоретических Y, т.е. случайную вариацию.

Общая дисперсия

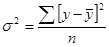
(8.19)

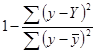характеризует размер отклонений эмпирических значений результативного признака у от 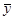, т.е. общую вариацию. Отношение случайной дисперсии к общей характеризует долю случайной вариации в общей вариации, а

(8.20.)

есть не что иное, как доля факторной вариации

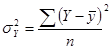(8.21)

в общей, потому что по правилу сложения дисперсий об­щая дисперсия равна сумме факторной и случайной дис­персий:

s=s_Y²+s₀² (8.22)

Подставим в формулу индекса корреляции соответству­ющие обозначения случайной, общей и факторной дис­персий и получим:

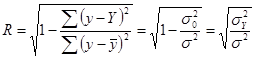(8.23)

Таким образом, индекс корреляции характеризует долю факторной вариации в общей:

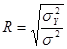(8.24)

однако с той лишь разницей, что вместо групповых сред­них берутся теоретические значения Y.

Индекс корреляции по своему абсолютному значению колеблется в пределах от 0 до 1. При функциональной зависимости случайная вариация å(y-Y)²=0, индекс корреляции равен 1. При отсутствии связи R = 0, потому что Y = у.

Коэффициент корреляции является мерой тесноты связи только для линейной формы связи, а индекс корреля­ции — и для линейной, и для криволинейной. При прямо­линейной связи коэффициент корреляции по своей абсо­лютной величине равен индексу корреляции:

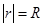(8.25)

Если индекс корреляции возвести в квадрат, то полу­чим коэффициент детерминации

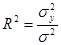(8.26)

Он характеризует роль факторной вариации в общей вариации и по построению аналогичен корреляционному отношению з². Как и корреляционное отношение, коэф­фициент детерминации R² может быть исчислен при по­мощи дисперсионного анализа, так как дисперсионный анализ позволяет расчленить общую дисперсию на фак­торную и случайную. Однако при дисперсионном анализе для разложения дисперсии пользуются методом группи­ровок, а при корреляционном анализе — корреляционны­ми уравнениями.

Коэффициент детерминации является наиболее конк­ретным показателем, так как он отвечает на вопрос о том, какая доля в общем результате зависит от фактора, поло­женного в основание группировки.

При прямолинейной парной связи факторную диспер­сию можно определить без вычисления теоретических зна­чений Y по следующей формуле:

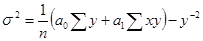(8.27)