Изучение основной тенденции развития
Тренд – долговременная компонента ряда динамики, она характеризует основную тенденцию его развития, при этом остальные компоненты рассматриваются только как мешающие процедуре его определения. При наличии ряда наблюдаемых значений для различных моментов времени следует найти подходящую трендовую кривую, которая сгладила бы остальные колебания.
После установления тенденции в ряду динамики, производится ее описание с помощью методов сглаживания. Методы сглаживания разделяются на две основные группы:
1. сглаживание или механическое выравнивание отдельных членов ряда динамики с использованием фактических значений соседних уровней,
2. выравнивание с применением кривой, проведенной между конкретными уровнями, т.о., чтобы она отображала тенденцию, присущую ряду, и одновременно освободила его от незначительных колебаний.
Рассмотрим некоторые из них.
· Метод усреднения по левой и правой половине
Разделяют ряд на две части, находят для каждой из них среднее арифметическое значение и проводят через полученные точки линию тренда на графике.
· Метод укрупнения интервалов
Если рассматривать уровни экономических показателей за короткие промежутки времени, то в силу влияния различных факторов, действующих в разных направлениях, в рядах динамики наблюдаются снижение и повышение этих уровней. Это мешает видеть основную тенденцию развития изучаемого явления. Поэтому для наглядного представления тренда применяется метод укрупнения интервалов, основанный на укрупнении периодов времени, к которым относятся уровни ряда. Например, ряд ежесуточного выпуска продукции заменяется рядом месячного выпуска продукции и т.д.
· Метод простой скользящей средней
Сглаживание ряда динамики с помощью скользящей средней заключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем – средний уровень такого же числа уровней, начиная сов второго, далее – начиная с третьего и т.д. Т.о., при расчетах среднего уровня как бы «скользят» по ряду динамики от его начала к концу, каждый раз отбрасывая один уровень в начале и добавляя один следующий. Каждое звено скользящей средней – это средний уровень за соответствующий период, который относится к середине выбранного периода. Применяется, если графическое изображение ряда динамики напоминает прямую линию.
· Метод центрирования
Определение скользящей средней по четному числу членов ряда динамики несколько сложнее, т.к. средняя может быть отнесена только к середине между двумя датами, находящимися в середине интервала сглаживания. Чтобы ликвидировать такой сдвиг, применяют способ центрирования. Центрирование заключается в нахождении средней из двух смежных скользящих средних для отнесения полученного уровня к определенной дате. При центрировании необходимо находить скользящие суммы, скользящие средние нецентрированные по этим суммам и средние из двух смежных нецентрированных скользящих средних.
· Метод взвешенной скользящей средней
Отличается от простой скользящей средней тем, что уровни входящее в интервал усреднения суммируется с различными весами.
· Выбор уравнения тренда, отображающего развитие социально – экономических явлений во времени.
Для отображения основной тенденции развития явлений во времени применяются полиномы разной степени.
- полином первой степени 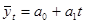 (9.18.)
(9.18.)
-полином второй степени 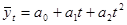 (9.19.)
(9.19.)
-полином третьей степени 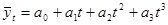 (9.20.)
(9.20.)
полином n – й степени 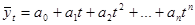 (9.21.)
(9.21.)
где а0, а1, а2, …, аn- параметры полиномов,
n – условное обозначение времени.
Суть способа: нахождение такой прямой или кривой, ординаты точек которой были бы максимально близки к уравнениям исследуемого динамического ряда.
Закономерно изменяющийся уровень изучаемого общественного явления ( 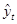 ) рассчитывается как функция времени(тренд):
) рассчитывается как функция времени(тренд):
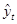 = f(t). (9.22.)
= f(t). (9.22.)
Параметры аналитического уравнения выбранной линии находят, используя способ наименьших квадратов. Предполагается, что сумма квадратов отклонений фактических уровней (у) от выровненных ( 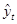 ), т.е. расположенных на искомой линии, должна быть минимальной:
), т.е. расположенных на искомой линии, должна быть минимальной:
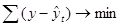 (9.23.)
(9.23.)
Рассмотрим технику выравнивания ряда динамики по уравнению тренда прямой:
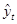 = а0 + а1t (9.24.)
= а0 + а1t (9.24.)
t – условное обозначение времени ;
а0 ;а1 – параметры искомой прямой.
Выравнивание по уравнению тренда прямой применяется в тех случаях, когда характер движения изучаемого явления ближе всего к прямолинейному. Для этого типа динамики характерны постоянные цепные абсолютные приросты: 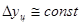
Параметры а0 ,а1, удовлетворяющие методу наименьших квадратов, находятся путем решения следующей системы нормальных уравнений:
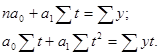
y – фактические уровни ряда динамики;
n – число уровней ряда;
t – нумерация фактора времени.
Эта система уравнений значительно упрощается, если значения t подобрать, чтобы их сумма = 0. Тогда получается следующая система уравнений:
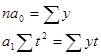 ,
,
решая которую получаем:
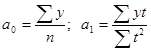 .
.
Если уровней нечетное число, то отсчет ведется от середины, принятой за 0:
| Год | |||||
| t | -2 | -1 |
Если уровней нечетное число, то условное обозначение времени t принимает следующий вид:
| Год | ||||||
| t | -5 | -3 | -1 |
а0 - среднее значение динамического ряда
а1 – ежегодный абсолютный прирост выравненного уровня, обусловленный изменением фактора времени t.
Дата добавления: 2016-07-22; просмотров: 2740;











