При этом токи и напряжения в частях схемы, не затронутых преобразовани-

ем, должны оставаться неизменными.

Находят токи в свернутой схеме. Затем возвращаются к исходной схеме с определением остальных токов.

Преобразование схемы проводят постепенно, рассматривая участки с последовательными и параллельными соединениями приемников. Предвари-

тельно нужно выявить узлы и ветви. Элементы, принадлежащие одной ветви,

соединены между собой последовательно. В них один ток. Эквивалентное

сопротивление последовательно соединенных резисторов равно сумме их со-

противлений:

.

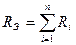При параллельном соединении элементы схемы замещения находятся под одним напряжением и соединены между собой двумя выходными зажимами. Эквивалентная проводимость параллельно соединенных резисторов

равна сумме их проводимостей:

.

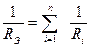В свернутой схеме ток определяют по закону Ома:

I = E / R_э.

При возвращении к исходной схеме с определением остальных токов удобно пользоваться формулой для определения тока в одной из двух парал-

лельно соединенных пассивных ветвей.

Ток в одной из двух параллельно соединенных пассивных ветвей про-

порционален току в неразветвленной части схемы. В числителе коэффициен-

та пропорциональности записывают сопротивление другой пассивной ветви,

в знаменателе – сумму сопротивлений двух пассивных ветвей.

ЛЕКЦИЯ 4. МЕТОДЫ РАСЧЕТА ТОКОВ

План лекции

1. Метод эквивалентных преобразований для расчета схем с трехполюсниками

2. Метод наложения

3. Метод эквивалентного генератора

1. Метод эквивалентных преобразований для расчета схем с трехполюсниками.

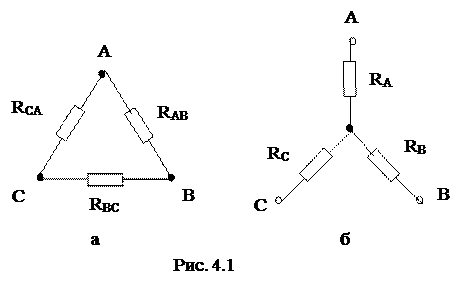
Если схема не содержит последовательные и параллельные соединения

резисторов, необходимо соединение треугольником (рис. 4.1, а), заменить

эквивалентной ему звездой (рис. 4.1, б) или выполнить обратную замену.

Структура формул эквивалентных преобразований имеет вид:

; ; ;

; ;

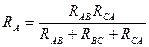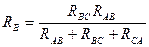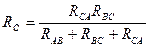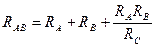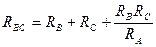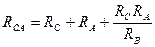
После преобразования резисторы в схеме соединены последовательно-

параллельно, их можно заменить одним с эквивалентным сопротивлением.

2. Метод наложения

Метод наложения основан на принципе независимости действия источников энергии. Ток в любой ветви схемы равен алгебраической сумме токов, возникающих в этой ветви под действием каждого отдельно работающего источника.

Схему делят на столько подсхем, сколько источников энергии. В каждой подсхеме оставляют только один источник, остальные источники ЭДС

закорачивают, источники тока – разрывают. Приемники во всех подсхемах остаются неизменными .Токи в подсхемах ищут методом эквивалентных преобразований.

Токи в схеме вычисляют алгебраическим суммированием токов в подсхемах.

Метод наложения рационально применять, если в схеме не больше

трех источников энергии.

Рассмотрим применение метода на конкретном примере.

Пример. Вычислить токи в схеме рис. 4.2, если известны значения ЭДС

источников и сопротивления всех резисторов.

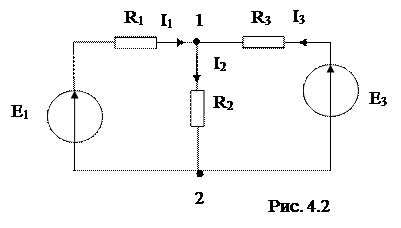1. Выявим узлы (1, 2), ветви, направим токи.

2. Разобьем схему на две подсхемы (рис. 4.3, а, б).

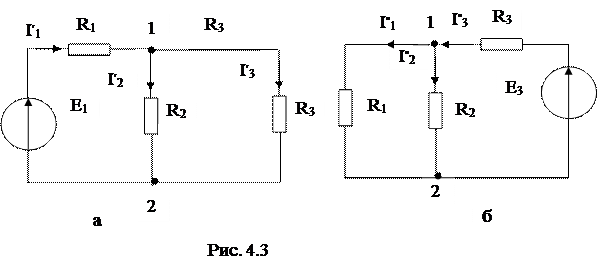
3. Выявим узлы и ветви в первой подсхеме. Ток I₁′ появляется в источ-

нике ЭДС, затем в узле 1 разветвляется на токи I₂′ и I₃′ . Направления токов

нужно указывать правильно. В подсхеме нет ветвей, содержащих больше од-

ного резистора, т. е. нет последовательных соединений. Резисторы с сопро-тивлениями R₂ и R₃ соединены параллельно. Их можно заменить одним ре-

зистором с эквивалентным сопротивлением R₂₃ =(R₂ R₃ )/( R₂ + R₃ ).

После этого преобразования схема превращается в последовательное

соединение с R_э′ = R₁ + R₂₃.

В свернутой схеме ток I₁′ вычислим по закону Ома: I₁′ =E₁ / R^׳_Э .

Ток I₂′ найдем по формуле разброса: I₂′ =(R₃ I₁′ )/( R₂ + R₃ ).

Ток I₃′ можно определить с помощью первого закона Кирхгофа:

I₃′ = I₁′ − I₂′ .

4. Выявим узлы и ветви во второй подсхеме, правильно направим токи.