ЛЕКЦИЯ 3. МЕТОДЫ РАСЧЕТА ТОКОВ
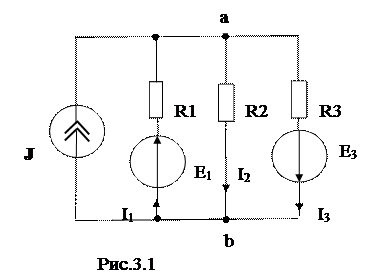
4. Составим (n −1) = 2 −1=1 уравнение по первому закону Кирхгофа:
J + I1 − I2 − I3 = 0
либо I1 − I2 − I3 = −J .
5. Дописываем два недостающих уравнения по второму закону Кирхгофа. Рекомендуют составлять уравнения для «главных», не содержащих в
себе других контуров. Направление обхода разных контуров может быть раз-
ным.
Выберем направление обхода контуров по часовой стрелке. Тогда
U1 +U2 = E1;
−U2 +U3 = E .
 |
Подставив выражения напряжений по закону Ома, получим следующую систему уравнений:
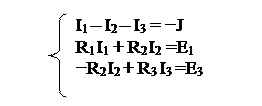
6. Решением системы находим токи.
Систему уравнений по законам Кирхгофа можно записать в матричной форме следующим образом:
[a]⋅[I ]= [F],
где [a] – квадратная матрица коэффициентов; [I ] – матрица-столбец неиз-
вестных токов ветвей; [F] – матрица-столбец активных параметров, которы-
ми являются токи источников тока и ЭДС.
Уравнения в системе не однотипны, так как записаны на основании двух разных законов. В уравнениях по первому закону Кирхгофа коэффициенты aij безразмерны и могут принимать значения ±1 или 0. В правой части Fj = ΣJ .
В уравнениях по второму закону Кирхгофа коэффициенты aij имеют размерность сопротивления, Fi = ΣE . Если j – ветвь входит в i -тый контур, для которого составлено уравнение, то aij = ±Rij , не входит – aij = 0 .
Для рассмотренного примера
| –1 | –1 | I1 | –J | |||||||||||||||
| [ | а | ] | = | R1 | R2 | ; | [ | I | ] | = | I2 | ; | [ | F | ] | = | E1 | |
| −R2 | R3 | I3 | E3 |
Расчет по законам Кирхгофа является универсальным, но громоздким.
Поэтому на его основе разработаны методы, позволяющие упростить решение.
2. Метод узловых потенциалов.
В качестве промежуточных неизвестных принимают потенциалы узлов.
Потенциал – функция многозначная, поэтому потенциал одного из уз-
лов принимают равным нулю. Рационально заземлять узел, в котором схо-
дится максимальное число ветвей.
Уравнения составляют на основании первого закона Кирхгофа. В них
подставляют значения токов, выраженные по закону Ома для активной и пас-
сивной ветвей. Число уравнений равно числу незаземленных узлов. Систему
можно записать в трафаретном виде:
где G11 , G22 , ..., Gmm – собственные проводимости узлов, равные сумме проводимостей ветвей, соединяющихся в соответствующем узле; G12 , G21 ,
G13 , ... – общие проводимости между двумя узлами, равные сумме проводи-
мостей ветвей, соединяющих эти узлы; J11, J22 , ..., Jmm – узловые токи, рав-
ные алгебраической сумме произведений проводимостей активных ветвей на
ЭДС этих ветвей и токов источников тока, соединяющихся в этом узле.
С положительным знаком берут ЭДС и токи, направленные к узлу.
Составим систему уравнений для схемы на рис. 3.2:
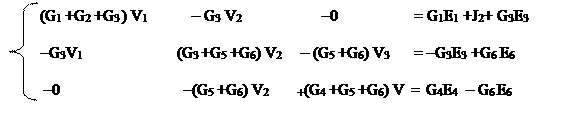
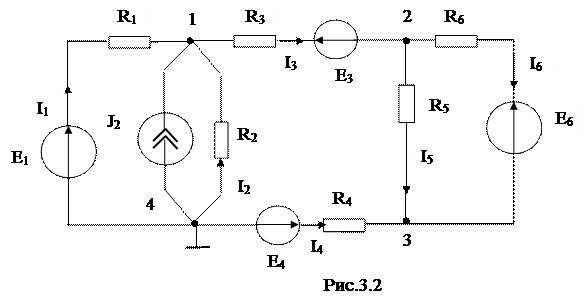 |
Решением системы уравнений определим потенциалы узлов. Затем рассчитаем токи ветвей по закону Ома:
I1 = G1(V4 −V1 + E1) = G1( −V1 + E1) , так как V4 = 0 ;
I2 = −G2V1 ; I3 = G3(V1 −V2 − E3); I4 = G4( −V3 + E4 ) ;
I5 = G5(V2 −V3); I6 =G6(V2 −V3 − E6).
3. Метод напряжения между двумя узлами.
Этот метод является частным случаем метода узловых потенциалов и применим для схемы с двумя узлами.
Так как потенциал одного из узлов принимают равным нулю, то потенциал второго узла равен напряжению между этими узлами.
Если принятьV2 = 0 , то трафаретная система даёт одно уравнение:
G11V1 = J11, гдеV1 =U12 .АСЧЕТА ТОКОВ
Формулу для определения напряжения между двумя узлами в общем виде можно записать следующим образом:
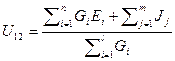
где Gi − проводимости ветвей; n − число ветвей, содержащих источники ЭДС с отличными от нуля проводимостями; m − число ветвей, содержащих источники тока; l − число ветвей без источников тока.
Число слагаемых в числителе равно числу активных ветвей. С положительным знаком записывают Е и J, направленные к первому в индексе напряжения узлу. Сумма в знаменателе формулы – арифметическая.
Вычислив напряжение между двумя узлами, по закону Ома для ветви находят токи.
4. Метод эквивалентных преобразований схем с последовательно параллельным соединением приемников.
Метод эквивалентных преобразований применяют как самостоятельный для расчета токов в схемах с одним источником энергии и несколькими приемниками. Его можно использовать и для упрощения частей сложной схемы при расчетах другими методами.
Все приемники заменяют одним с эквивалентным сопротивлением.
Дата добавления: 2020-10-14; просмотров: 598;











