Мінімізація логічних функцій
Зведення логічної функції до УДНФ або до УКНФ дає однозначне зображення 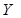 . Однак для технічної реалізації такої логічної функції властивість однозначності зображення буде зручним тільки в тому випадку, якщо повним набором логічних елементів є елементарний базис, що складається з окремих елементів І, АБО, НЕ, причому з числом входів елементів І та АБО, що дорівнює рангу термів логічної функції. На практиці часто доводиться будувати цифрові пристрої на різних базисах, і тоді з’ясовується, що удосконалені форми зображення логічних функцій не завжди найекономніші. Їм властива надлишковість, яка підлягає спрощенню, тобто мінімізації. Цій процедурі, до речі, можуть підлягати логічні функції інших, не обов’язково удосконалених, форм зображення.
. Однак для технічної реалізації такої логічної функції властивість однозначності зображення буде зручним тільки в тому випадку, якщо повним набором логічних елементів є елементарний базис, що складається з окремих елементів І, АБО, НЕ, причому з числом входів елементів І та АБО, що дорівнює рангу термів логічної функції. На практиці часто доводиться будувати цифрові пристрої на різних базисах, і тоді з’ясовується, що удосконалені форми зображення логічних функцій не завжди найекономніші. Їм властива надлишковість, яка підлягає спрощенню, тобто мінімізації. Цій процедурі, до речі, можуть підлягати логічні функції інших, не обов’язково удосконалених, форм зображення.
Мінімізація - це процес зведення логічної функції до такого виду, який припускає більш просту і дешеву її фізичну реалізацію, тобто з меншим числом логічних елементів за рахунок зменшення числа логічних символів, кількості змінних та зв’язків між елементами.
Відомо кілька методів мінімізації, серед яких найбільш поширеними в інженерній практиці є такі:
· безпосередніх перетворень;
· карт Карно;
· Квайна.
Знайти гарантовано мінімальний вираз для довільної логічної функції можна лише методом повного перебору в процесі мінімізації всіх можливих варіантів. Від руки (на папері) це реально здійснити для невеликої кількості змінних. Із збільшенням числа змінних складність розглянутих методів мінімізації зростає за геометричною прогресією і стає під силу лише автоматизованим методам, які призначені для ЕОМ.
Для оцінки складності логічної функції, яка зображена тою чиіншою формою, вводиться поняття ціни реалізації (покриття) логічної функції. За Квайном ціна покриття логічної функції визначається числомзмінних (букв) в конституенті, що рівнозначно числу входів логічних елементів, які реалізують задану функцію. Кон’юнкціі вищого рангу покриваються відповідними кон’юнкціями нижчого рангу. Наприклад, кон’юнкції 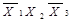 і
і 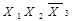 покриваються кон’юнкціею
покриваються кон’юнкціею 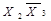 .
.
В загальному випадку операцію покриття зображає операція склеювання (див. табл.1.3) 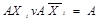 , де
, де 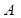 - елементарна кон’юнкція або імпліканта. тобто така логічна функція, яка отримана в результаті склеювання і яка на будь-якому наборі змінних
- елементарна кон’юнкція або імпліканта. тобто така логічна функція, яка отримана в результаті склеювання і яка на будь-якому наборі змінних 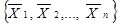 набуває такого самого значення, що й сама функція (конституента), що її утворила. Чим. більше число покриттів, що знижують ранг імпліканти, тим простіший кінцевий вираз. Прості імпліканти – це елементарні кон’юнкції (що мають менше число членів, ніж змінних) найнижчого рангу, які входять у дану логічну функцію. Якщо в днз’юнкції простих імплікант жодну з них шляхом поглинання вилучити (покрити) не вдається, таку диз’юнкцію називають тупиковою, або мінімізованою диз’юнктивно-нормальною формою (МДНФ) заданої функції.
набуває такого самого значення, що й сама функція (конституента), що її утворила. Чим. більше число покриттів, що знижують ранг імпліканти, тим простіший кінцевий вираз. Прості імпліканти – це елементарні кон’юнкції (що мають менше число членів, ніж змінних) найнижчого рангу, які входять у дану логічну функцію. Якщо в днз’юнкції простих імплікант жодну з них шляхом поглинання вилучити (покрити) не вдається, таку диз’юнкцію називають тупиковою, або мінімізованою диз’юнктивно-нормальною формою (МДНФ) заданої функції.
Таким чином, загальною задачею мінімізації логічних функцій є знаходження скороченої ДНФ, тобто знаходження всіх простих імплікант, визначення серед них тупикових ДНФ і, нарешті, вибір з останніх мінімальних, які утворюють МДНФ заданої логічної функції.
Метод безпосередніх перетворень - це аналітичний метод спрощення логічних функцій з допомогою аксіом та законів бульової алгебри (див. табл.1.4). При набутті певних навичок цей метод є досить ефективним для малої кількості змінних (як правило, не більше трьох).
Для мінімізації логічних функцій методом безпосередніх перетворень корисно використовувати такі формули бульової алгебри:
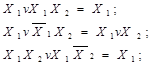
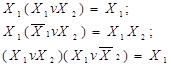
У деяких випадках ефективніше мінімізувати інверсію логічної функції для отримання простішого виразу в МДНФ. Це може бути тоді, коли логічна функція має переважаюче число одиниць, ніж нулів. Тоді, маючи МДНФ інверсної функції, при технічній реалізації цієї функції достатньо на виході побудованої схеми під’єднати інвертор для відновлення прямої функції.
Приклад: Отримати МДНФ для логічної функції, що задана таблицею істинності (див. табл. 1.9).
Таблиця 1.9 Таблично задана логічна функція
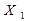
| 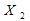
| 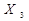
| 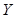
|
Розв’язання. Оскільки у даній функції число одиниць переважає над числом нулів, виконаємо мінімізацію для її інверсії:
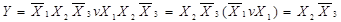
Отже, 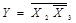 . Порівняємо з МДНФ прямої функції:
. Порівняємо з МДНФ прямої функції:
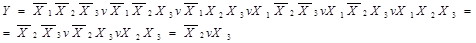
Приклад : Методом безпосередніх перетворень мінімізувати логічну функцію
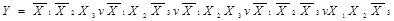
Розв’язання:
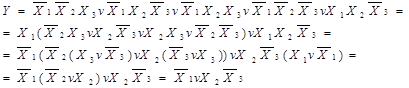
Дата добавления: 2016-07-22; просмотров: 10247;











