Основні поняття та закони бульової алгебри
У зв’язку з двійковим зображенням цифрових сигналів, що набувають тільки двох значень /0 і 1/, найзручнішим математичним апаратом для аналізу та синтезу цифрових систем є алгебра логіки (бульова алгебра). У бульовій алгебрі символи 0 і 1 характеризують стани змінних та їх функцій і тому не можна розглядати ці символи як арифметичні числа. Алгебра логіки - це алгебра станів, а не алгебра чисел, і їй властиві, на відміну від звичайної алгебри- логічні дії над станами.
Основне поняття алгебри логіки - висловлення, тобто речення, в якому міститься суть (сенс) твердження істинності або його заперечення (хибності). Будь-яке висловлення можна позначити символом, наприклад, X або У , і вважати, що, Х = 1 або У = 1, якщо висловлення істинне, а X = 0 або У=0, якщо висловлення неістинне (хибне). Оскільки будь-яка змінна (або її функція) може мати стан 0 або 1, в алгебрі логіки кожній двійковій змінній ставиться у відповідність обернена до неї (інверсна) змінна, така, що якщо Х=0, то 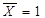 , а якщо
, а якщо 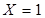 , то
, то 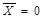 . Подвійне заперечення дав аргумент, тобто
. Подвійне заперечення дав аргумент, тобто 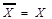 . Риска "-" над змінною Х означає, що над змінною
. Риска "-" над змінною Х означає, що над змінною 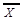 здійснено операцію логічного заперечення. Ця елементарна і дуже важлива у бульовій алгебрі логічна операція називається інверсією (логічним запереченням). Вона означає, що якщо висловлення (
здійснено операцію логічного заперечення. Ця елементарна і дуже важлива у бульовій алгебрі логічна операція називається інверсією (логічним запереченням). Вона означає, що якщо висловлення ( 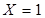 ) істинне, то висловлення "НЕ X" (
) істинне, то висловлення "НЕ X" ( 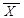 ) - хибне (
) - хибне ( 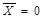 ), а якщо висловлення X - хибне (
), а якщо висловлення X - хибне ( 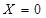 ), то висловлення
), то висловлення 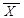 - істинне (
- істинне ( 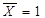 ).
).
Логічна функція 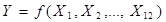 - це складне висловлення з кількох простих, які пов’язані між собою логічними операціями. Логічна функція
- це складне висловлення з кількох простих, які пов’язані між собою логічними операціями. Логічна функція 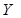 набуває значення 0 або 1 (
набуває значення 0 або 1 ( 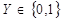 ) при наборі логічних двійкових змінних (аргументів)
) при наборі логічних двійкових змінних (аргументів) 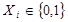 .
.
Якщо кожному значенню аргументу відповідає тільки одне значення логічної функції, така функція називається однозначною, якщо два або більше - багатозначною. Однозначна функція 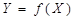 може бути зображена тільки двома аргументами (0 і 1) і двома своїми значеннями (0 і 1). Отже, число однозначних функцій у цьому випадку може бути тільки 22=4. Особливо цікава одна з них - інверсія
може бути зображена тільки двома аргументами (0 і 1) і двома своїми значеннями (0 і 1). Отже, число однозначних функцій у цьому випадку може бути тільки 22=4. Особливо цікава одна з них - інверсія 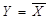 , решта - тривіальні.
, решта - тривіальні.
Вхідний набір - це певна комбінація значень двійкових змінних 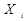 . у логічній функції У . Максимальне число вхідних наборів визначається як
. у логічній функції У . Максимальне число вхідних наборів визначається як 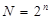 (де n - число змінних), максимальне число логічних функцій n змінних - як
(де n - число змінних), максимальне число логічних функцій n змінних - як 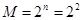 .
.
Двозначні функції 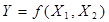 мають N=4 можливих значень аргументів /
мають N=4 можливих значень аргументів / 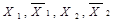 / і два різних значення функцій (
/ і два різних значення функцій ( 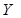 і
і 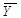 ), що в результаті дає 24=16 різних двозначних бульових функцій. Число наборів аргументів 22=4. а їх значення такі:
), що в результаті дає 24=16 різних двозначних бульових функцій. Число наборів аргументів 22=4. а їх значення такі: 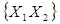 ,
, 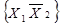 ,
, 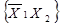 ,
, 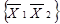 . У випадку функції трьох змінних
. У випадку функції трьох змінних 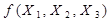 різних наборів аргументів буде
різних наборів аргументів буде
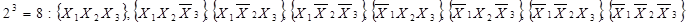 а різних значень тризначної функції буде вже 28=256.
а різних значень тризначної функції буде вже 28=256.
Логічна функція, яка має певні значення 0 або 1 на всіх вхідних наборах, називається повністю визначеною функцією. Якщо логічна функція мав значення, які на деяких вхідних наборах не визначені, їх називають байдужими (або непевними). Частково визначену логічну функцію можна зробити повністю визначеною (довизначеною) приписуванням байдужим наборам довільних значень функції.
Множину логічних Функцій 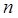 змінних можна утворити з допомогою трьох основних логічних операцій:
змінних можна утворити з допомогою трьох основних логічних операцій:
· логічного заперечення (“-”) - інверсії;
· логічного додавання (“v”) – диз’юнкції;
· логічного множення (“.”) кон’юнкції.
Для згаданих операцій справедливі такі аксіоми (тотожності або правила):
· універсальна множина –{ 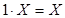 ; 1vX=1;}
; 1vX=1;}
· нульова множина -{ 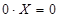 ; 0vX=X;}
; 0vX=X;}
· повторення (тавтологія) -{ 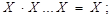 XvXv…vX=X;}
XvXv…vX=X;}
· доповнення –{Ошибка! Объект не может быть создан из кодов полей редактирования.; XvОшибка! Объект не может быть создан из кодов полей редактирования.;}
· подвійна інверсія - 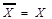 .
.
В алгебрі логіки діє принцип дуальності, згідно з яким дві функції рівносильні одна одній, якщо на всіх можливих наборах змінних вони набувають одного і того самого значення, тобто 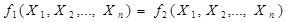 . Принцип дуальності (двоїстості) є основним принципом бульової алгебри. Він має велике практичне значення, що визначило одну з переваг цифрової техніки. Застосовуючи його, можна будувати нові логічні функції, логічні елементи та пристрої, причому досить просто. Властивість дуальності /двоїстості/ бульової функції е основою наступних двох правил бульової алгебри:
. Принцип дуальності (двоїстості) є основним принципом бульової алгебри. Він має велике практичне значення, що визначило одну з переваг цифрової техніки. Застосовуючи його, можна будувати нові логічні функції, логічні елементи та пристрої, причому досить просто. Властивість дуальності /двоїстості/ бульової функції е основою наступних двох правил бульової алгебри:
правило К. Шеннона стверджує, що для одержання алгебраїчного виразу інверсної функції необхідно у згаданій функції всі змінні замінити на інверсні їм, всі знаки кон’юнкції - на знаки диз’юнкції, а всі знаки диз’юнкції - на знаки кон’юнкції;
правило де Моргана стверджує, що інверсія кон’юнкції дорівнює диз’юнкції інверсій, а інверсія диз’юнкції – кон’юнкції інверсій.
У бульовій алгебрі також діють закони, за якими можна встановити аналітичні зв’язки між різними логічними функціями і виконувати відповідні перетворення для спрощення складних виразів. Основні закони бульової алгебри зведені в табл.1.4. Справедливість аксіом і законів легко перевірити прямою підстановкою нуля або одиниці на місце конкретного аргументу.
Таблиця 1.4 Основні закони булевої алгебри
| Закони комутативності /переміщення/ | 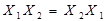
 v v 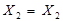 v v 
|
| Закони асоціативності /сполучення/ | 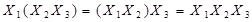
 v v 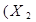 v v 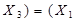 v v 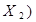 v v 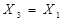 v v  v v 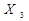
|
| Закони дистрибутивності /розподілу/ | 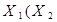 v v 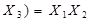 v v 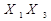
 v v 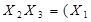 v v 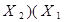 v v 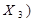
|
| Закони склеювання | 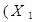 v v 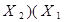 v v 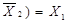
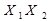 v v 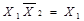
|
| Закони поглинання | 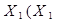 v v 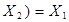
 v v 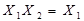
|
| Закони дуальності /правило де Моргана/ | 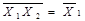 v v 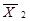
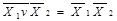
|
Застосовуючи аксіоми (тотожності) та закони бульової алгебри, можна отримати нові логічні формули, а також довести справедливість того чи іншого закону на основі інших.
Особливої уваги заслуговують закони дуальності (правило де Моргана), з допомогою яких кон’юнкцію можна виразити через диз’юнкцію, і навпаки. Таку операцію часто треба здійснювати при перетвореннях Логічних виразів. Корисними для практики можуть бути також наслідки законів дуальності, зокрема:
 v
v 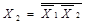 ; ( 1.0)
; ( 1.0)
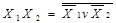 ; ( 1.0)
; ( 1.0)
Закони дуальності та наслідки з них справедливі для довільного числа змінних:
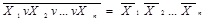 ;
; 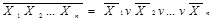 ;
;
Дата добавления: 2016-07-22; просмотров: 3141;











