Форми зображення логічних функцій
Будь-яку логічну функцію можна задати або зобразити у різних формах: словесно, таблично, числового запису, аналітичне і координатної карти чи діаграми. Розглянемо кожну з цих форм окремо.
Словесне зображення - це логічне висловлення, під яким розуміють довільне твердження, щодо якого можна сказати, істинне воно або хибне. Наприклад, функцію 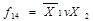 - імплікацію від
- імплікацію від  до
до 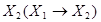 словесно можна зобразити (описати) так (див. табл. 1.5): функція
словесно можна зобразити (описати) так (див. табл. 1.5): функція 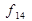 хибна тоді і тільки тоді, коли
хибна тоді і тільки тоді, коли  істинне і
істинне і  хибне.
хибне.
Табличне зображення характеризується таблицею істинності,якамає 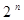 рядків за числом вхідних наборів,
рядків за числом вхідних наборів, 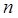 - стовпців за числом змінних
- стовпців за числом змінних 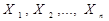 т - стовпців за числом функцій (
т - стовпців за числом функцій ( 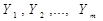 ).У випадку однозначної функції число стовпців таблиці істинності дорівнюєn+ 1,а для багатозначної функції n+ т. Приклад однозначної функції трьох змінних
).У випадку однозначної функції число стовпців таблиці істинності дорівнюєn+ 1,а для багатозначної функції n+ т. Приклад однозначної функції трьох змінних 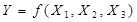 , яку зображено таблицею істинності, наведеної у табл. 1.7. Функцію, зображену таблицею істинності, можна також "читати" аналогічно, як при словесному зображенні.
, яку зображено таблицею істинності, наведеної у табл. 1.7. Функцію, зображену таблицею істинності, можна також "читати" аналогічно, як при словесному зображенні.
Таблиця 1.7 Таблично задана логічна функція
| Номер набору |  
| 
| 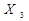
| 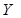
|
Кожний спосіб чи форма зображення має свою специфіку і тому буде зручною там, де даний спосіб є найбільш простимчикомпактним. Таблична форма запису хоча й наочна і може бути застосована для довільного числа змінних, однак при аналізі властивостей функції такий записне є компактним. Для випадку чотирьох і більше змінних табличне зображення логічної функції е суттєво складнішим та громіздким. Простішим буде числовий запис, коли логічна функція задається у вигляді послідовності десяткових чисел, що є еквівалентами тих вхідних наборів, на яких дана функція набуває значення 1 або 0. Наприклад, таблицю істинності (табл. 1.7) легко переписати у числову, форму: для вхідних наборів, на яких 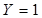 . маємо
. маємо 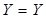 (0,3,4,7), а для наборів, на яких
(0,3,4,7), а для наборів, на яких 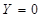 , маємо
, маємо 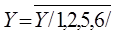 або для
або для 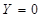 маємо
маємо 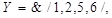 а для
а для 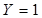
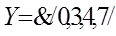 , де кожний з записів повністю зображує логічну функцію, подану табл. 1.7, і, як бачимо, а більш компактним.
, де кожний з записів повністю зображує логічну функцію, подану табл. 1.7, і, як бачимо, а більш компактним.
При аналітичному зображенні функція задається алгебраїчним виразом, який отримують при застосуванні логічних операцій до змінних бульової алгебри. Якщо попередні форми зображення логічної функції лише вказують значення функції на конкретних наборах змінних, то аналітичне зображення, крім того, ще дозволяє виконувати різні аналітичні перетворення, які необхідні як для аналізу, так і для синтезу цифрового пристрою, що реалізує або має реалізувати дану логічну функцію.
Нехай на фіксованому вхідному наборі { 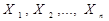 } задана логічна функція
} задана логічна функція 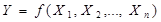 . Оскільки кожна змінна
. Оскільки кожна змінна 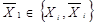 =
= 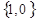 ,набір значень змінних, очевидно, є конкретним двійковим числом
,набір значень змінних, очевидно, є конкретним двійковим числом 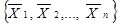 . За номер вхідного набору можна взяти довільне число
. За номер вхідного набору можна взяти довільне число
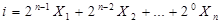
В інших випадках, наприклад, коли набір 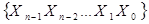 зображує двійкове число, більш зручним є запис номера набору як:
зображує двійкове число, більш зручним є запис номера набору як:
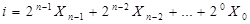
Найбільш раціональним е зображення логічних функцій в так званих нормальних (канонічних) формах запису, зокрема, у вигляді диз’юнкції кон’юнкцій або кон’юнкції диз’юнкцій змінних, що взяті з інверсіями або без них. Окремі вирази функції змінних 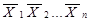 називають термами, а самі (однозначні) функції
називають термами, а самі (однозначні) функції 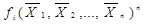 -конституентами.
-конституентами.
Кон’юнктивний терм (мінтерм або конституента одиниці) 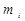 - це терм, що зв’язує всі змінні, які зображені у прямій або у інверсній формі знаком кон’юнкції, причому
- це терм, що зв’язує всі змінні, які зображені у прямій або у інверсній формі знаком кон’юнкції, причому
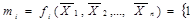 , якщо номер набору дорівнює
, якщо номер набору дорівнює 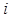 ;
;
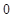 , якщо номер набору не дорівнює
, якщо номер набору не дорівнює 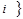 ;
;
Наприклад: 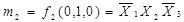
Або 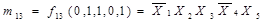
Диз’юнктивний терм (макстерм або конституента нуля) 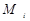 - це терм, що зв’язує всі змінні, які зображені у прямій або уінверсній формі знаком диз’юнкції, причому
- це терм, що зв’язує всі змінні, які зображені у прямій або уінверсній формі знаком диз’юнкції, причому
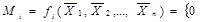 ,якщо номер набору дорівнює
,якщо номер набору дорівнює 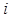 ;
;
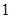 , якщо номер набору не дорівнює
, якщо номер набору не дорівнює 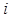 ;
;
Наприклад: 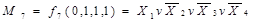
Або 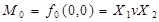
Ранг терма 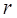 визначається кількістю змінних, які входять у даний терм. Наприклад, мінтерм
визначається кількістю змінних, які входять у даний терм. Наприклад, мінтерм 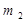 має
має 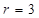 , а
, а 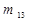 має
має 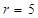 , макстерм
, макстерм 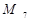 має
має 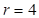 , а
, а 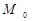 має
має 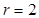 .
.
Згідно із законом дуальності будь-яку логічну функцію 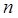 змінних можна зобразити як диз’юнкцію кон’юнкцій (мінтерм) або як кон’юнкцію диз’юнкцій (макстерм) змінних. Однозначне зображення логічних функцій одержують тільки при так званих удосконалених нормальних формах (УНФ), тобто таких, при яких мінтерми або макстерми формуються з усіх аргументів логічної функції і є одного (причому максимального) рангу. Якщо логічна функція складається з набору диз’юнкцій елементарних кон’юнкцій одного рангу, її називають удосконаленою диз’юнктивно-нормальною формою (УДНФ), а якщо з набору кон’юнкцій елементарних диз’юнкцій - удосконаленою кон’юнктивно-нормальною формою (УКНФ) зображення. Для
змінних можна зобразити як диз’юнкцію кон’юнкцій (мінтерм) або як кон’юнкцію диз’юнкцій (макстерм) змінних. Однозначне зображення логічних функцій одержують тільки при так званих удосконалених нормальних формах (УНФ), тобто таких, при яких мінтерми або макстерми формуються з усіх аргументів логічної функції і є одного (причому максимального) рангу. Якщо логічна функція складається з набору диз’юнкцій елементарних кон’юнкцій одного рангу, її називають удосконаленою диз’юнктивно-нормальною формою (УДНФ), а якщо з набору кон’юнкцій елементарних диз’юнкцій - удосконаленою кон’юнктивно-нормальною формою (УКНФ) зображення. Для 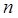 -змінних складається
-змінних складається 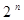 мінтерм
мінтерм 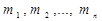 (при УДНФ) або
(при УДНФ) або 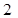 макстерм
макстерм 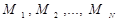 (при УКНФ).
(при УКНФ).
В загальному випадку алгебраїчний вираз логічної функції в УДНФ
набував вигляду
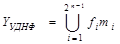 (1.5)
(1.5)
де 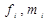 - значення функції (0або 1) та мінтерма на
- значення функції (0або 1) та мінтерма на 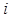 -му наборі змінних.
-му наборі змінних.
В УКНФ загальний вираз логічної функції
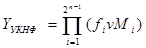 (1.6)
(1.6)
де 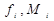 - значення функції (0 або 1) та макстерма на
- значення функції (0 або 1) та макстерма на 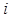 -му наборі змінних.
-му наборі змінних.
Застосовуючи закони алгебри логіки (див. табл.1.4), неважко довести еквівалентність обох форм зображення будь-якої логічної функції. Такі форми зображення логічних функцій необхідні при проектуванні цифрових пристроїв.
Для згаданого прикладу (див. табл.1.7) можна записати два тотожних (дуальних) вирази логічної функції. Беручи лише до уваги конституенти1, маємо
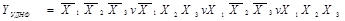
а для конституент 
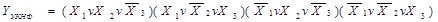
Отже, якщо логічну функцію задано таблично, то для переходу до її аналітичного зображення в УНФ роблять так:
для зображення в УДНФ описують ті набори змінних, для яких . функція дорівнює одиниці, тобто для конституент І; для кожного такого набору складають мінтерм, причому змінні 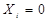 замінюють на
замінюють на 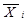 і одержані мінтерми з’єднують диз'юнкціею;
і одержані мінтерми з’єднують диз'юнкціею;
для зображення в УКНФ виписують набори, для яких функція дорівнює нулю, тобто для констатуент 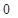 для кожного набору складають макстерм, причому змінні
для кожного набору складають макстерм, причому змінні 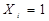 замінюють на
замінюють на 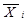 і одержані макстерми об’єднують кон'юнкцією.
і одержані макстерми об’єднують кон'юнкцією.
Приклад: Утворити УДНФ логічної функції, що задана в ДНФ:
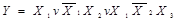
Розв’язання. Для підвищення рангу кон’юнкції молодшого рангу застосовуємо доповнення типу 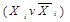 :
:
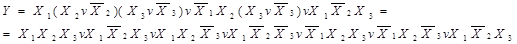
Приклад: Таблично-задану логічну функцію 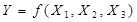 записати в аналітичній формі (див.табл. 1.8) для тотожних зображень УДНФ та УКНФ.
записати в аналітичній формі (див.табл. 1.8) для тотожних зображень УДНФ та УКНФ.
Розв’язання. В УДНФ:
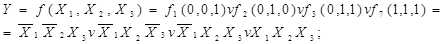
В УКНФ:
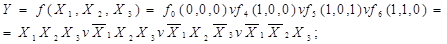
Таблиця 1.8 Таблично задана логічна функція.
| Номер набору | 
| 
| 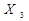
| 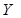
|
Слід зауважити, що в даному прикладі вибір форми зображення логічної функції не має принципового значення, бо число мінтерм дорівнює числу макстерм. Проте у випадках, коли число одних переважав над числом інших, наприклад, кількість 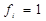 більша за кількість
більша за кількість 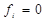 , або навпаки, тоді менш громіздким буде функція з меншим числом терм.
, або навпаки, тоді менш громіздким буде функція з меншим числом терм.
Приклад: Перейти до УКНФ логічної функції, що задана в УДНФ
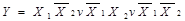
Розв’язання. Спочатку спростимо вираз за законом склеювання:
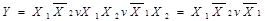
Застосувавши правило Шеннона, маємо
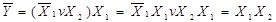
За принципом подвійної інверсії та законом дуальностіостаточно одержимо
Дата добавления: 2016-07-22; просмотров: 4375;











