Використання базових логічних елементів

Разом з однофункціональними елементами (HI,I,АБО), широко використовуються двофункціональні (I-HI,АБО-HI,ВИКЛ. АБО). Більш обмежено використовуються трьохфункціональні (I-АБО-HI) з різним рівнем розширення. Вказаний набір комбінаційних мікросхем з повного набору серії, що зветься бібліотекою, є базовим набором або базовими логічними елементами. Більш того, проектовані матричні великі інтегральні схеми (BIC) орієнтуються також на використання логічних функцій, тотожних базовим логічним елементам.

Серед задач, які часто зустрічаються при проектуванні логічних схем, слід виділити наступні:

· реалізація функцій у базисах I-HI,АБО-HI;

· розширення логічних можливостей елементів.

Задача реалізації логічних функцій розв’язується шляхом використання правила подвійного заперечення та теореми де Моргана. Проілюструємо це на наступних прикладах.

Приклад 2.9. Використовуючи елементи I-HI, реалізувати функцію:

.

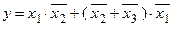(2.4)

Розв’язання. На основі правила подвійного заперечення функція (2.4) може бути зображена у вигляді:

.

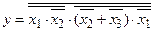Враховуючи, що 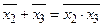, логічну схему можемо зобразити у вигляді, приведеному на рис. 2.4.

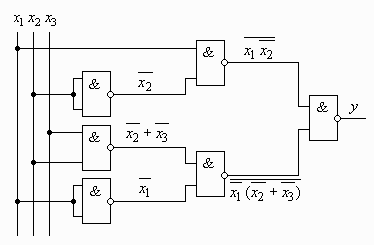
Рис.2.4.

Приклад 2.10. Використовуючи елементи АБО-HI, реалізувати функцію:

.

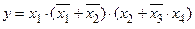(2.5)

Розв’язання. За аналогією з попереднім прикладом, вираз зобразимо у вигляді:

.

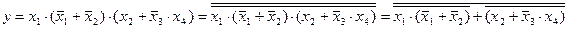Реалізація функції (2.5) приведена на рис. 2.5. Враховано, що

; .

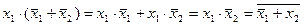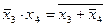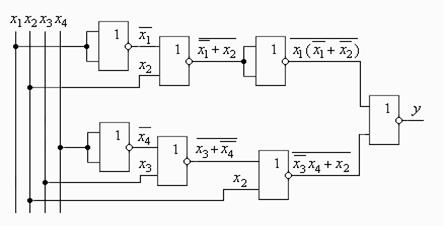
Рис.2.5.

Приклад 2.11. Побудувати схему знаходження суми за модулем 2 на вісім входів, використовуючи двовходові елементи, які реалізують таку функцію.

Розв’язання. Елементи ВИКЛ.АБО реалізують наступну логічну функцію:

.

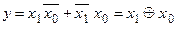Логічна функція, реалізацію якої поставлено задачею, має вигляд:

.

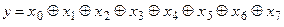(2.6)

Для побудови пристрою, що реалізує функцію (2.6), скористаємось сполучним законом, завдяки якому виконаємо два варіанти перетворень:

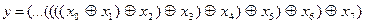;	(2.7)
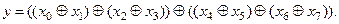
	(2.8)

Формула (2.7) дає можливість створити послідовну схему (рис. 2.6, a); (2.8) – відповідно, пірамідальну (рис. 2.6, б). Обидві схеми по апаратних затратах еквівалентні. Але величини часових затримок у них суттєво різні.

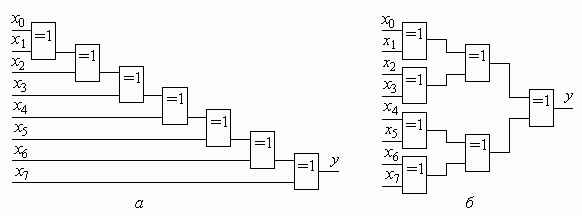
Рис.2.6.

У першому випадку величина затримки виконання операції t_З пов’язана з затримкою елемента t_З0 та їх кількістю m співвідношенням:

.

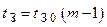При пірамідальному з’єднанні величина t_З суттєво менша і знаходиться за формулою:

.

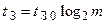Перша з розглянутих схем (рис. 2.6) використовується, наприклад, для виділення фронту та спаду імпульсу, а також для подвоєння частоти імпульсів.

Ці властивості ілюструються схемою та часовими діаграмами, що приведені на рис. 2.7, a, б. Елементи DD1.1…DD1.3 виконують затримку імпульсу U_вх на величину 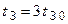, а DD1.4 виділяє імпульси U_вих відповідно до логіки роботи елемента.

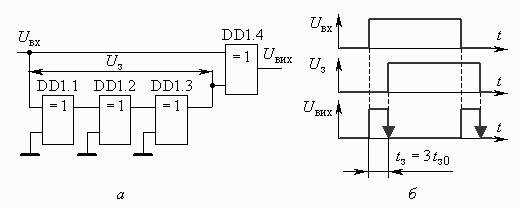
Рис.2.7.

Схема, приведена на рис. 2.6, б, є основою схем, призначених для перевірки на парність багаторозрядних цифрових слів, які широко використовуються в комп’ютерній техніці.

Приклад 2.12. Використовуючи елементи ВИКЛ. АБО, розробити схему пристрою для вмикання (вимикання) освітлення в приміщенні з трьома входами, біля кожного з яких повинен розміщуватись вимикач.

Розв’язання. Складаємо таблицю станів функції, що реалізується пристроєм, прийнявши за логічні змінні стани вимикачів – відповідно x₂ , x₁ , x₀ (див. табл. 2.4).

Прийнявши, що при вимкнених вимикачах лампочка освітлення не горить, тобто y = 0 при x₀ = 0, x₁ = 0, x₂ = 0, істинні значення функції будуть лише при непарній кількості ввімкнених вимикачів, тобто для мінтермів з порядковими номерами 1, 2, 4, 7.

Логічна функція буде описуватись наступним виразом:

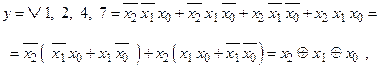
оскільки

.

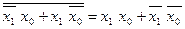Схема пристрою може бути реалізована за одним з двох варіантів, приведених на рис. 2.6, а, б.

Мультиплексори

При передачі цифрової інформації виникає велика кількість ситуацій, коли цифровий двійковий код необхідно перетворити з паралельного формату в послідовний з метою його запису або передачі по двопроводній лінії. Як приклад, пристрої запису інформації – накопичувачі на компакт-дисках, гнучкі та жорсткі диски – використовують послідовний формат. З послідовним форматом працюють COM-порти ПЕОМ, модеми, USB-шини.

Розглянемо умови і принцип перетворення двійкового коду з паралельного формату у послідовний.

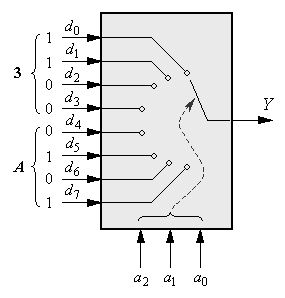
	Таблиця 2.5.
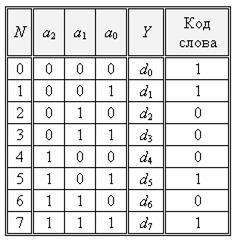
Рис.2.8.

Припустимо, що по однобайтовій шині даних до пристрою підводиться двійкове слово d₇ d₆ d₅ d₄ d₃ d₂ d₁ d₀ = A3₁₆ (рис. 2.8), яке пристрій повинен зчитати і передати в послідовному форматі на вихід Y.

Щоб виконати таку операцію, необхідно послідовно звертатись (адресуватись) до кожного біта даних і по черзі приєднувати його до виходу Y. Зрозуміло, що для забезпечення такої адресації необхідно мати три розряди адресної шини. У механічному еквіваленті адресна шина визначає короткочасне положення бігунка перемикача, який по черзі з’єднує вхід шини даних з виходом Y пристрою.

Роботі пристрою, що зображений на рис. 2.8, відповідає таблиця станів (табл. 2.5).

Якщо вихідний код Y розглядати як функцію вхідних сигналів пристрою, то отримаємо наступну залежність:

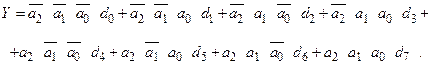
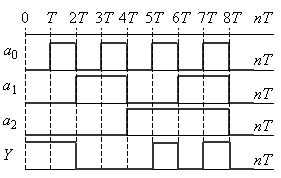
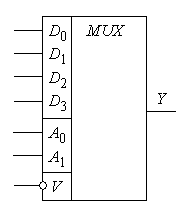
Якщо зміну сигналів a₂ , a₁ , a₀ забезпечити послідовно в часі з тактовим інтервалом Т, то можемо побудувати часову діаграму (рис. 2.9), яка встановлює послідовність передачі сигналів на входах d₇…d₀ на вихід Y.

Звідси витікає, що мультиплексор – це цифровий комбінаційний пристрій, який забезпечує перетворення інформації, що задана на входах d₇…d₀ у паралельному форматі, в послідовний формат на виході Y.

Рис.2.9.	Рис.2.10.

Умовне позначення мультиплексора в електронних схемах приводиться на рис. 2.10. Входи А називають адресними (адресна шина), а входи D – входами даних (шина даних). Допоміжний вхід V називають керуючим або дозволяючим. З його урахуванням робота мультиплексора, приведеного на рис. 2.10, описуватиметься наступною логічною функцією:

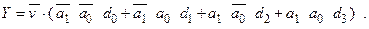
(2.9)

Дозволяючий вхід V розширює можливості пристрою. Він дає можливість синхронізувати роботу мультиплексора з іншими схемами, а також використовується для нарощування розрядності адресних сигналів. Логічна схема мультиплексора, реалізована у базисі елементів І-АБО-НІ у відповідності до формули (2.9), приведена на рис. 2.11.

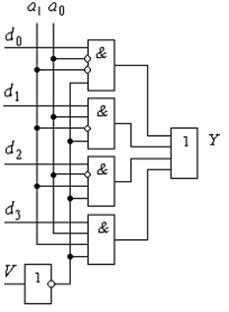
Рис.2.11.

Кількість входів шини даних мультиплексора відображається у його назві. Наприклад, розглянута схема відповідає назві “з чотирьох в один”, або просто “4:1”. В залежності від кількості інформаційних входів, вони бувають “8:1”, “16:1” і т. д.

Технічні характеристики мультиплексорів визначаються статичними й динамічними характеристиками базових ЛЕ відповідних серій з урахуванням складності схеми.

Оскільки мультиплексор є пристроєм логіки, то на його базі можуть реалізовуватись різні логічні функції. Як приклад, скористаємось формулою (2.9). Припустимо, що необхідно реалізувати логічну функцію:

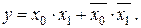
(2.10)

Порівнюючи формули (2.9) і (2.10), бачимо, що, присвоївши адресним сигналам a₀ , a₁ значення x₀ , x₁ відповідно і забезпечивши виконання умов d₁ = d₂ = 0, d₀ = d₃ = 1, v = 0, одержимо схему пристрою (рис. 2.12), який реалізує функцію (2.10).

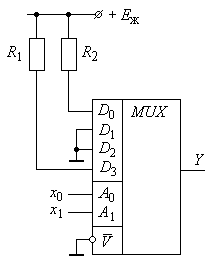
Рис.2.12.

Нескладні перетворення логічних функцій дають можливість реалізовувати на мультиплексорах функції з кількістю змінних, що перевершує кількість адресних входів. Виконується наступна послідовність перетворень:

· у мінімізованій диз’юнктивній нормальній формі функції виділяються змінні, які мають найвищий ранг, тобто повторюються в найбільшій кількості диз’юнкцій. Наприклад, вибирається m змінних;

· виконується перетворення функції так, щоб забезпечити присутність виділених змінних в усіх диз’юнкціях. Для цього кожна диз’юнкція домножається на ;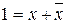

· проводиться перегрупування змінних логічної функції таким чином, щоб виділені змінні були винесені за дужки у відповідних групах диз’юнкцій.

У результаті виконаних перетворень одержується формула вихідної функції, яка реалізується на мультиплексорі “з M = 2^m в 1”, якщо на його адресні входи подати виділені змінні, а на інформаційних входах забезпечується виконання тих логічних виразів, які залишились в дужках. Якщо вирази в дужках є функціями декількох змінних, то їх реалізація може бути забезпечена або за допомогою іншого мультиплексора, або на основі типових логічних елементів.

Приклад 2.13. Функцію п’яти змінних:

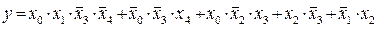
реалізувати з використанням мультиплексора “з 4-х в 1”.

Розв’язання. У використовуваному мультиплексорі наявні два адресні входи – отже, вибираємо дві змінні з найбільшими рангами. Ранги змінних приведені в табл. 2.6.

Таблиця 2.6.

Вибираємо змінні x₂ та x₃ .

Виконуємо перетворення функції:

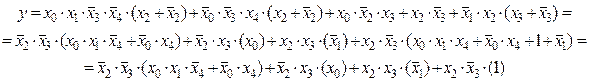
Логічна сума в перших дужках також реалізується за допомогою мультиплексора 4:1, якщо на адресні входи його подати змінні x₀ та x₄ .

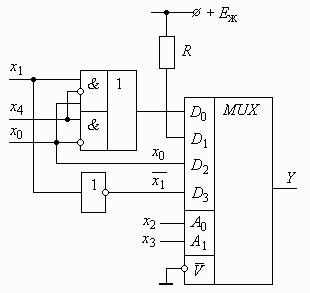
Рис.2.13.

Принципова схема пристрою, що реалізує потрібну логічну функцію, приведена на рис. 2.13.

У більшості серій мікросхем мультиплексори, що виготовляються у вигляді самостійних виробів, мають кількість інформаційних входів, не перевищуючу шістнадцяти. Збільшення їх кількості досягається різними прийомами з’єднання окремих мультиплексорів.

Для збільшення кількості інформаційних входів необхідно підвищувати кількість адресних провідників (ємність адресного простору, адресної шини). У схемі, приведеній на рис. 2.14, розширення адресного простору досягається використанням входу V, який, об’єднаний в обох мультиплексорах через інвертор DD3, виступає старшим розрядом адресної шини. При a₂ = 0 зміна сигналів на a₀ , a₁ дозволить вибирати входи d₀ …d₃ шини даних і через елемент АБО (DD4) передавати на вихід Y. Мультиплексор DD2 при цьому відключений високим рівнем сигналу на виході DD3. При a₂ = 1 зміною a₀ , a₁ забезпечується комутація входів d₄ …d₇ на вихід Y. При наявності в мультиплексорах інверсних виходів їх об’єднання забезпечується елементом І-НІ(DD5).

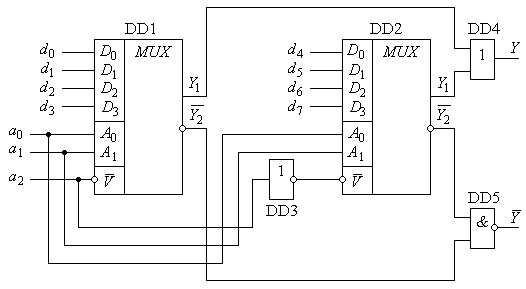
Рис.2.14.

При необхідності суттєвого нарощування кількості комутованих інформаційних входів використовується пірамідальний спосіб нарощування. Приклад його реалізації приведений на рис. 2.15. Ця схема в реалізації є більш гнучкою. Адресні входи мультиплексорів нижнього рівня DD1…DD4 з’єднуються паралельно і керуються молодшими розрядами адресного простору. Їх кількість визначається тільки кількістю інформаційних входів кожного мультиплексора. Мультиплексор верхнього ступеня задає старші розряди адресного простору, завдяки яким він забезпечує комутацію виходу кожного з мультиплексорів Y₀ …Y₃ на загальний вихід Y.

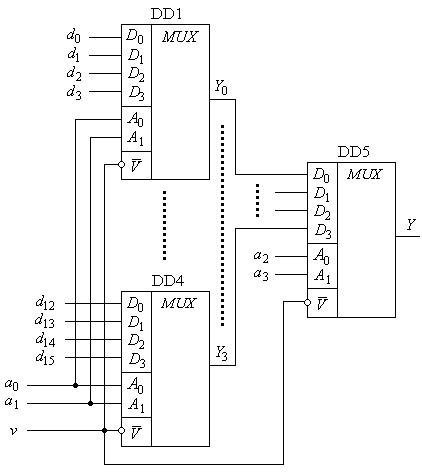
Рис.2.15.

При використанні інших комбінаційних пристроїв – наприклад, дешифраторів, про які мова піде нижче – з’являються більш широкі можливості нарощування розрядності інформаційної та адресної шин мультиплексорів.