Перетворення числової інформації

У процесі перетворення інформації, яку несуть цифрові сигнали, у цифровій системі (пристрої) виникає необхідність переводу чисел з однієї системи числення в іншу еквівалентну систему. Це означав що, наприклад, десятковому числу А має відповідати двійкове число А₂

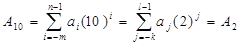(1.2)

де aj = 0,1,2,...,9 - цифра в і-му розряді (m+n) -розрядного числа А10; аj=0 або aj=1 – цифр в j-му розряді (k+l) -розрядного двійкового числа A2 .

Перевід чисел з будь-якої позиційної системи числення у код "10" вже розглядався у підрозд.1.1. Для цього досить скористатися виразом (1.1), з допомогою якого розрахована сума ряду дає шуканий результат.

Розглянемо тепер перевід чисел у різних системах числення. Загальним правилом переводу числа з однієї системи числення до іншої е виконання таких послідовних кроків:

1) ділення в цілих числах заданого числа AР на основу Р тої системи, в яку переводиться дане число АР ;

2) якщо частка не дорівнює нулю, її слід взяти за нове число і повторити операцію п.1; якщо частка дорівнює нулю, перейти до п.3;

З) виписати всі остачі у зворотному порядку, починаючи з останньої, і взяти їх за цифри шуканого числа an-1 an-2 … a1 a0

За такими самими правилами виконуються взаємні перетворення (переводи) в інших системах числення. Тільки при цьому ділити або множити потрібно на число, яке дорівнює основі тієї системи числення, до якої треба перейти. Розглянемо приклад переводу числа 118₁₀ з десяткової системи числення в двійкову:

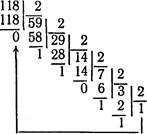
Записуючи неподільну частку і залишки в порядку, зворотному їхній появі, знаходимо що 118₁₀=1110110₂