Задачі, які розв’язуються методами теорії потоків

Дано спочатку формулювання основних задач, які розв’язуються за допомогою алгоритму знаходження максимального потоку.

Транспортна задача. Є m пунктів відправки і n пунктів призначення вантажу. Задаються вартості перевезень між кожними пунктами відправлення і призначення, кількість наявних транспортних засобів в кожного пункту призначення. Потрібно скласти план перевезення вантажу, який забезпечує мінімальні витрати. Особливістю задачі є те, що розв’язок повинен бути цілочисельним.

Задача про попит і пропозицію. Оптовий торгівець в кожний з N послідовних інтервалів може купляти, продавати і зберігати (щоб продати пізніше) деякий товар. При цьому в кожний і-й період задаються: а_і – верхня границя кількості товару, більше якої він купити не може; верхня границя с_ікількості товару, яку він зберегти, і нижня границя в_і кількості товару, яку він може продати. Задані вартості придбання, продажу і зберігання в кожний і-й період. Потрібно визначити оптимальну політику поведінки торгівця при якій він отримає максимальний прибуток за N періодів.

Задача про оптимальне використання шляхів. З різних міст 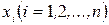і пункт призначення у відправляються машини (при заданій наявній кількості машин а_і в пункті х_і). Відомі тривалості t_ij руху автомашин між пунктами х_і і х_j; максимальна кількість автомашин с_ij, яку може пропустити кожна дорога і максимальна кількість машин с_kr, яка може знаходитися в пункті х_r. потрібно скласти план руху таким чином, щоб за час Т в пункті призначення прибула максимальна кількість машин.

Задача про найкоротший шлях. Хай задана транспортна мережа, в якій є джерело і виток. Для кожної дуги вказується вартість проїзду (може бути довжина чи вартість проїзду).

Потрібно знайти шлях, який з’єднує початкову і кінцеву точку, сумарна вартість проїзду по якому мінімальна.

Задача про склад. Задана місткість складу; кількість товару, яка розміщена на складі на початку діяльності; ціни на товари, які купляються і продаються в кожний і-й період часу і витрати за цей період, які пов’язані зі зберіганням одиниці товару. Потрібно визначити оптимальні кількості товару, які повинні бути куплені і продані в різні періоди часу 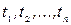таким чином, щоб сукупний прибуток за N періодів був максимальним.

Задача про оптимальний по вартості сітковий графік. Задається сітковий графік праці з загальної вартістю 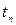. Вважається, що для кожної роботи, яка представляється дугою, залежність її вартості від тривалості роботи є лінійною. Потрібно мінімізувати загальну вартість проекту при заданій загальній тривалості робіт.