Анализ точности методами математической

Статистики

Погрешности, возникающие при обработке разделяют на:

- систематические постоянные;

- систематические закономерно изменяющиеся;

- случайные.

Систематические погрешности – погрешности, постоянные по значению и знаку или изменяющиеся по определенному закону.

Систематические постоянные погрешности – погрешности из-за неточности приспособления, станка, инструмента и др.

Систематические закономерно изменяющиеся погрешности – погрешности из-за износа инструмента, температурных деформаций системы и др.

Случайные погрешности – погрешности, не постоянные по значению и знаку.

Случайные погрешности – погрешности, вызванные неравномерной твердостью материала, колебаниями припуска, температурного режима, силой зажима заготовки в приспособлении и др.

Кривые распределения и оценка точности

На их основе

Статистический метод оценки точности применяется в условиях производства большого количества деталей на основе выборок на исследуемой операции. По результатам измерения деталей выборки строится опытная кривая распределения, к которой по критерию согласия подбирается теоретический закон распределения.

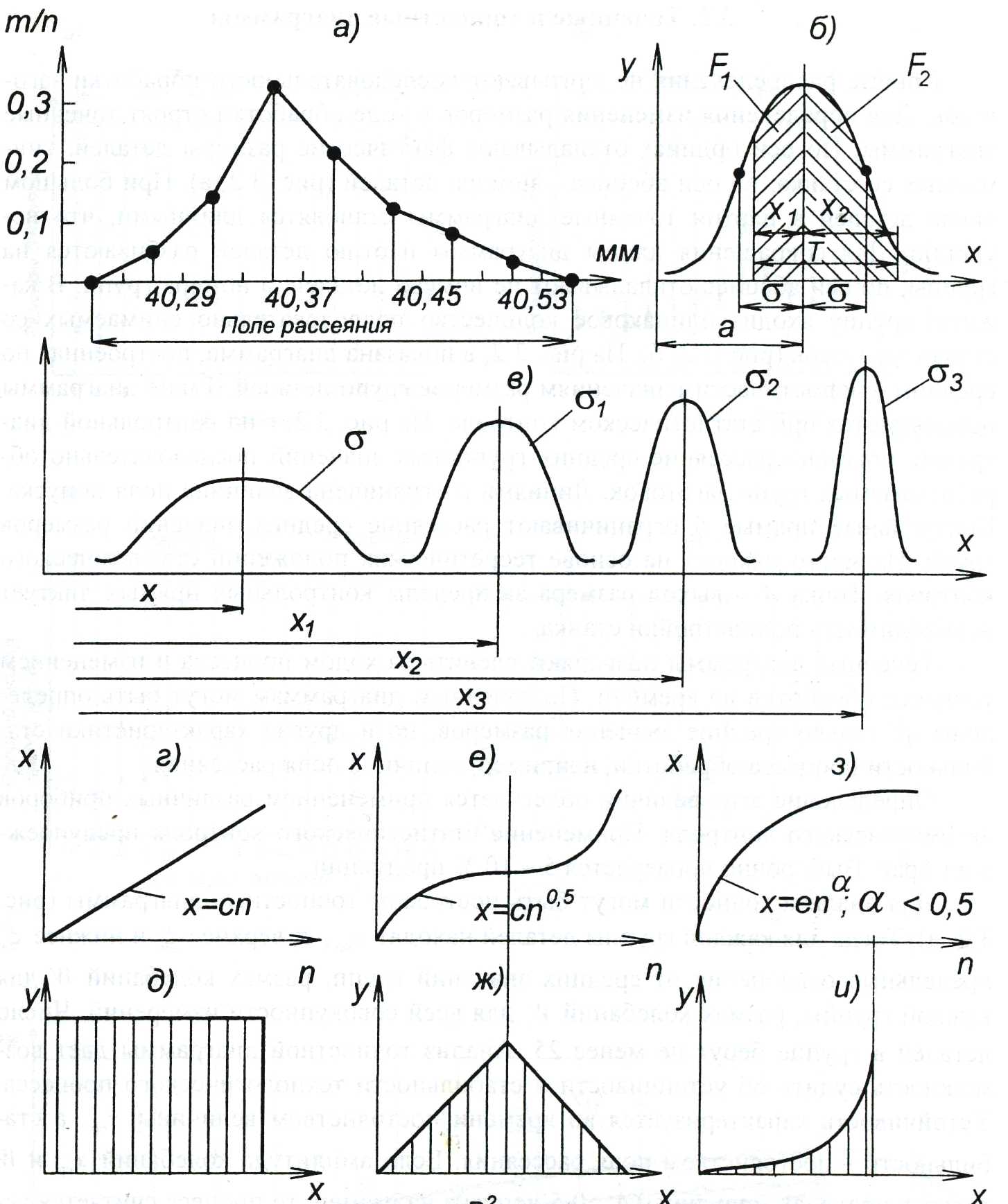
По оси абсцисс откладывается измеряемая величина через определенные интервалы, а по оси ординат их количество, попадающее в эти интервалы, или частости. Частость – это отношение числа деталей одного размера к общему числу деталей выборки. При соединении точек пересечений, получается ломаная линия, называемая опытной кривой распределения или полигоном распределения деталей по размерам (рис. 2.13,а). Определяется поле рассеяния размеров деталей как приближенная мера их точности.

Размеры деталей, высоты микронеровностей, погрешности измерений, распределения массы заготовок, твердости и других механических свойств распределяются наиболее часто по нормальному закону Гаусса. Кривая распределения представлена на рис. 2.13,б. Уравнение кривой Гаусса

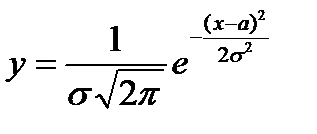, (2.21)

где 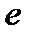- основание натуральных логарифмов;

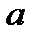- значение абсциссы, при которой ;

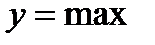- среднее квадратичное отклонение исследуемой величины,

Рис. 2.13. Кривые распределения и их разновидности

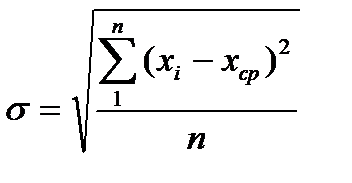, (2.22)

где 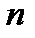- число измерений;

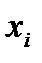- значение текущего измерения;

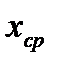- среднее арифметическое из произведенных измерений,

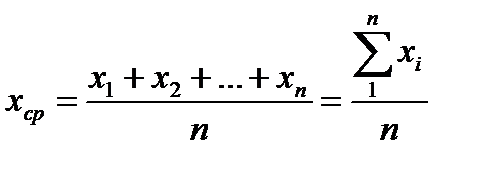. (2.23)

При 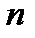= 50 погрешность определения равна 10 %, при 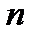= 25 она равна 15 %. При малом числе измерений

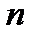
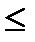10 вычисление дает большую ошибку.

При .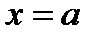

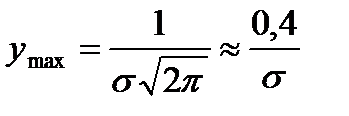Точки перегиба кривой лежат на расстоянии от оси симметрии, их ординаты .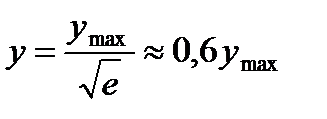

Среднее квадратичное отклонение является мерой точности обработки. На рис. 2.13,в показаны кривые распределения с 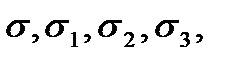характеризующие точность соответственно заготовки, после предварительной, чистовой и отделочной обработки. При правильно построенном ТП 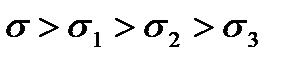, а величины 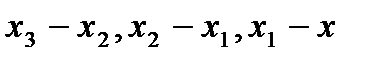должны быть во избежание брака достаточно большими.

Сравнение поле фактического рассеяния размеров деталей с заданным полем допуска, определяет возможность или целесообразность их обработки выбранным способом.

Кроме закона нормального распределения используются и другие законы. Если на размер обработки оказывает влияние установившийся износ инструмента, то распределение размеров деталей будут подчиняться закону равной вероятности (рис. 2.13, г, д). Если имеет место ярко выраженный приработочный износ, зона установившегося износа мала, а за ней идет зона ускоренного возрастания износа, распределение размеров может оказаться выраженным законом треугольника (Симпсона) (рис. 2.13, е, ж). При тепловых деформациях системы изменение размера обработки и распределение размеров деталей выражаются кривыми, изображенными на рис. 2.13, з, и.

Систематические постоянные погрешности не влияют на форму кривой распределения. Влияние этой погрешности выражается в том, что кривая распределения сдвигается на величину этой погрешности по оси абсцисс.

Систематические закономерно изменяющиеся погрешности искажают кривую распределения.

После построения опытных кривых распределения, используются критерии согласия Пирсона, В.И.Романовского, А.Н.Колмогорова, подбирают теоретический закон распределения.

Рис. 2.14. Точечная диаграмма

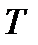По кривой распределения возможно нахождение вероятного процента годных деталей и брака. Если поле допуска (рис. 2.13,б) ограничено абсциссам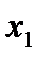и и 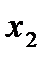, то вероятное количество годных деталей выразится отношением площаде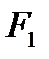й и 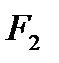к площади 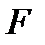, заключенной между кривой и осью абсцисс.

Метод кривых распределения универсален. Однако метод не учитывает последовательности обработки, фиксирует результаты законченного этапа, не дает информации для управления точностью процесса обработки.

Точечные диаграммы

В процессе обработки детали берутся со станка малыми текущими выборками (не менее 25) в течение рабочей смены через определенные промежутки времени (15…20 минут). Для каждой группы деталей находятся 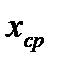, , верхнее 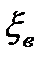и нижнее 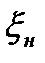предельные отклонения от средних значений групп, размах колебаний 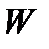для каждой группы, размах колебаний 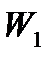для всей совокупности измерений. Для построения точечных диаграмм вычерчиваются графики, в которых по оси ординат наносятся значения 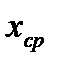, , , , 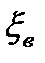, , 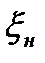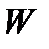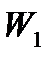а по оси абсцисс – время взятия выборки или их номера (рис. 2.14).

Диаграммы позволяют следить за изменением точности обработки во времени, судить об устойчивости и стабильности ТП. Устойчивость характеризуется во времени постоянством величины 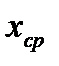, а стабильность – постоянством поля рассеяния. Если амплитуда колебани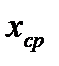й и 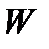лежат в пределах меньших 0,4…0,5 допуска на размер, то процесс считается устойчивым и стабильным. По диаграмме может быть выявлено влияние некоторых систематически изменяющихся погрешностей, например, наличие размерного износа режущего инструмента (рис. 2.14).