МАТЕМАТИЧЕСКАЯ МОДЕЛЬ БЕСПОДШИПНИКОВОЙ ИНДУКТОРНОЙ МАШИНЫ

<12 3 4 5 6 7 >

В настоящее время в некоторых специфических областях электропривода используются двигатели и генераторы с подвесом роторов в активных магнитных подшипниках (АМП) [1]. Магнитные силы притяжения, действующие на ротор со стороны электромагнитов, управляются с помощью электронной системы управления. Такая система естественно дороже обычных шарикоподшипников, однако она позволяет получить ряд неоспоримых преимуществ: практически неограниченный ресурс; снижение расходов на обслуживание; малый коэффициент трения; малая отдача теплоты в окружающую среду; возможность работы на высоких скоростях, в вакууме, при низких и высоких температурах, в условиях агрессивных сред, в сверхчистых технологиях; возможности создания контролируемых микроперемещений ротора в зазоре, системы активного гашения колебаний ротора; вращение ротора вокруг оси инерции (самоцентрирование ротора) и отсутствие вибраций вследствие дисбаланса; отсутствие шума и вибраций; контроль нагрузки на подшипники, положения ротора, дисбаланса и балансировки ротора. Данные преимущества позволяют использовать их во многих отраслях промышленности с достижением значительного экономического эффекта.

Развитием АМП является бесподшипниковая электрическая машина (БЭМ). Идея БЭМ состоит в том, чтобы объединить электродвигатель и АМП в одной машине. В этом случае в зазоре должно действовать такое электромагнитное поле, при взаимодействии которого с ротором возникали бы как вращающий момент, так и управляемые радиальные силы. Это позволяет уменьшить длину ротора, что главным образом сказывается на увеличении критических скоростей и расширении диапазона частот вращения, а также улучшении массово-габаритных показателей по сравнению с использованием АМП.

Существуют различные варианты исполнения БЭМ на основе электродвигателей различных типов: асинхронные двигатели, двигатели с постоянными магнитами, индукторные и другие, в которых нет механического контакта между статором и ротором. Описание их конструкции изложено в [2]. Каждый тип двигателя имеет как свои преимущества, так и недостатки. К преимуществам индукторного двигателя можно отнести простоту в изготовлении (в отличие от двигателей с постоянными магнитами), температурнонезависимыми (в отличие от двигателей с постоянными магнитами, в которых меняется магнитная проводимость от температуры и асинхронных, в которых меняется электрическая проводимость ротора). Однако индукторные двигатели обычно обладают меньшим значением КПД по сравнению с двигателями на постоянных магнитах.

В Псковской Инженерной Компании совместно с ОАО «Электропривод» г. Киров разработана бесподшипниковая индукторная машина (БПИМ) оригинальной конструкции.

Разрез данной бесподшипниковой индукторной машины представлен на рис. 1.

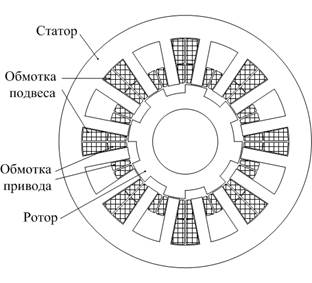
Рис. 1. Разрез бесподшипниковой индукторной машины

Обмотки привода располагаются в малых пазах статора.
Все секции обмотки привода включаются последовательно, согласно или встречно, в зависимости от направления потоков возбуждения, так чтобы наводимые в них МДС складывались.

При смене полярности тока в обмотке привода, изменяется поле, создаваемое этой обмоткой, а, следовательно, и распределение МДС под зубцами, что приводит к созданию вращающего момента.

Статор БЭМ имеет 16 полюсов, ротор – 8 полюсов. Статор имеет 5 однофазных обмоток: обмотка привода «m» и обмотки подвеса x1, x2, y1, y2. Обмотку привода образуют 16 катушек привода с числом витков 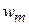каждая и с одинаковым током 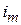и МДС .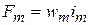

Подвес ротора в направлении оси x осуществляют обмотки x1 и x2, в направлении оси y – обмотки y1 и y2. Каждая из этих обмоток образована двумя катушками, намотанными на пару соседних полюсов с w_s витками. Токи в обмотках подвеса 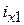, , 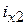, 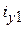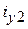создают МДС 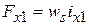, , 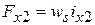, 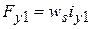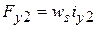. МДС катушек одной обмотки
имеют противоположное направление. Зубцовая полярность этих МДС:
N-N-N-N-S-S-S-S-….

Для всестороннего изучения и исследования данной машины необходимо получить для нее адекватную математическую модель.

Связь потокосцеплений обмотки привода 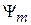и обмоток подвеса 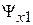, , 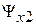, 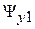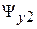с токами в обмотках привода 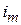и подвеса 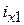, , 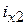, 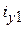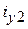выражается через матрицу индуктивностей L:

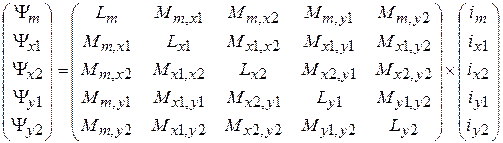, (1)

или

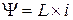где 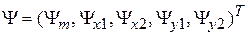, 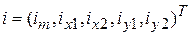– векторы-столбцы потокосцеплений и токов соответственно.

Для получения математической модели требуется найти выражения для самоиндуктивностей 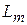, , 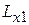, , 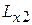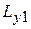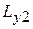и взаимоиндуктивностей , , , , , , , , , .

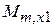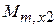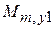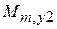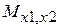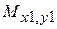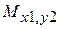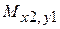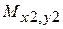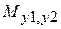Определение зависимостей индуктивностей от положения ротора. Схема замещения магнитной цепи БПИМ приведена на рис. 2.

На рис. 2 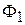,…, 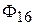– магнитные потоки через полюса, , …,
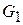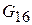– магнитные проводимости под полюсами.

Используя метод двух узлов, по которому магнитный поток через k-й полюс равен:

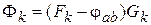, (2)

где 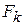- МДС k-й ветви, A; 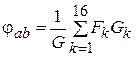- магнитный потенциал

между узлами «a» и « b», A; 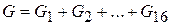- суммарная проводимость всех зазоров, Гн.

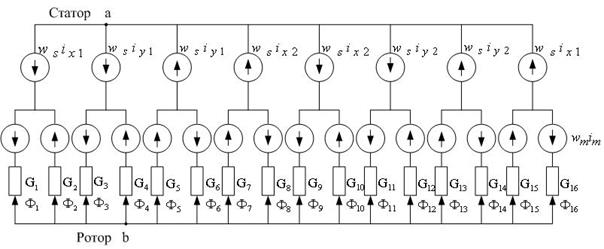
Рис. 2. Схема замещения магнитной цепи БПИМ

Для определения самоиндуктивности обмотки привода 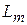найдем потоки 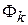и примем ток 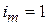, а токи .

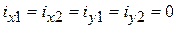Тогда собственная индуктивность обмотки привода вычисляется как:

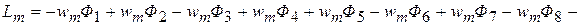
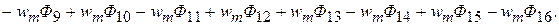(3)

Определив потоки по (2) и подставив их в (3) получим:

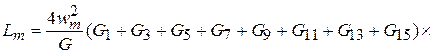
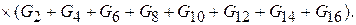
Аналогично определяются остальные индуктивности.

Для определения индуктивностей необходимо знать магнитные проводимости зазоров при различных положениях ротора.

Расчет проводимостей воздушных путей потока можно выполнить по приближенным формулам приведенным в [3].

Для двух перпендикулярных поверхностей: ,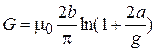

где а - ширина проводящего материала, м; b - длина, м; g - расстояние между поверхностями, м; 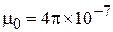Гн/м - магнитная постоянная. Для двух параллельных поверхностей: .

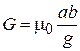Используя формулы, приведенные выше получена зависимость магнитной проводимости от смещения ротора относительно статора 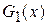(рис. 3, а)). Значения длины ротора 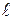=0,07 м, высоты воздушного зазора g=0,0003 м, ширины зубца t_п=0,006 м

Максимальная проводимость вычисляется по формуле:

.

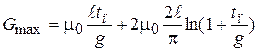Минимальная проводимость вычисляется по формуле:

.

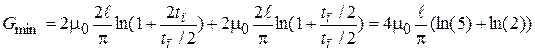Зависимость 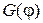весьма близка к косинусоиде:

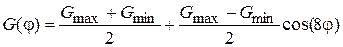. (4)

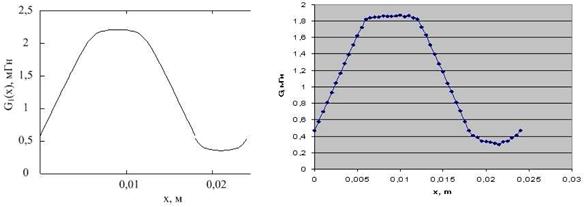
Для оценки полученных результатов было проведено моделирование проводимости методом конечных элементов в программной среде FEMM (рис. 3, б).

А б

Рис. 3. Зависимости магнитной проводимости от смещения ротора

Как видим, результаты расчетов различными методами весьма схожи. Для дальнейших расчетов аппроксимируем зависимость 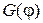косинусоидой (4).

Примем данную аппроксимацию к описанию проводимостей всех 16 полюсов. Учитывая, что зависимость величины зазора от углового положения и смещения ротора по осям х и у имеет вид [2]: 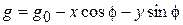, получим следующее выражение для максимальной проводимости k-го зубца статора:

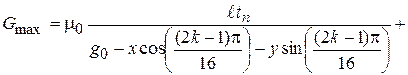
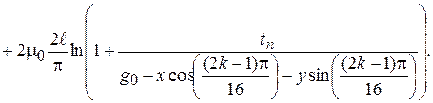
Учитывая аппроксимацию зависимости проводимость от угла поворота ротора косинусоидой, можно записать функцию :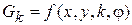

.

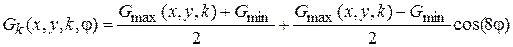Таким образом определены зависимости собственных и взаимных индуктивностей всех обмоток от радиального смещения и угла поворота ротора.

Определение вращающего момента и радиальных сил. Вращающий момент и радиальные силы БПИМ можно найти как частные производные от магнитной энергии по углу поворота ротора и радиальным смещениям.

Магнитная энергия находится по соотношению: 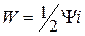. Учитывая то, что БПИМ представляет собой систему из пяти токовых контуров и используя выражение (1) можно записать:

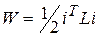. (5)

Раскрывая выражение (5) получим:

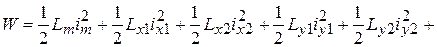
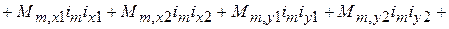
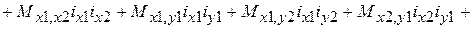
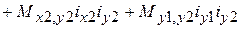. (6)

Здесь первая строка описывает магнитную энергию самоиндуктивностей, вторая строка – энергию взаимных индуктивностей обмотки привода и обмоток подвеса, третья и четвертая строки – энергию взаимных индуктивностей между обмотками подвеса. Подставляя полученные выражения индуктивностей в (6) определяем магнитную энергию системы:

.

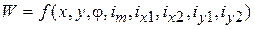Вращающий момент определяется как частная производная магнитной энергии W по углу вращения :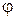

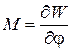. (7)

Радиальные силы F_x и F_y определяются как частные производные магнитной энергии по x и y соответственно:

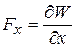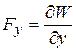, . (8)

Сравнение полученных результатов. В ходе работы была построена модель электромагнитной системы БПИМ в среде моделирования методом конечных элементов FEMM.

В ходе ее исследований были получены следующие зависимости:

а) силы по оси х_ от смешения ротора по оси х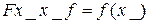

б) силы по оси х от тока в 1-й обмотке подвеса ;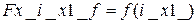

в) силы по оси y от тока в 1-й обмотке подвеса ;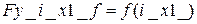

г) момента от угла поворота ротора .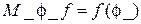

Для оценки адекватностей моделей построим данные зависимости используя данные модели, рассчитанной методом конечных элементов и модели, рассчитанной аналитически по (7) и (8) в среде Mathcad: 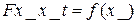, , 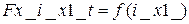, 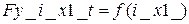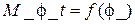. На рис. 4 показаны эти зависимости.

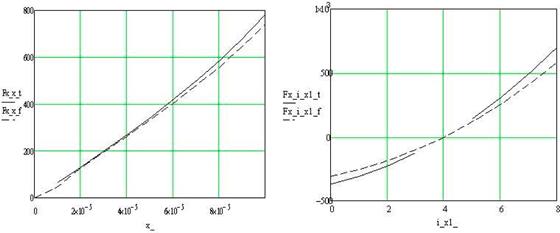
Из рис. 4 (а) видно, что на незначительных перемещениях ротора зависимость имеет практически линейный характер, причем результаты моделирования аналитическим методом и в среде FEMM практически полностью совпадают.

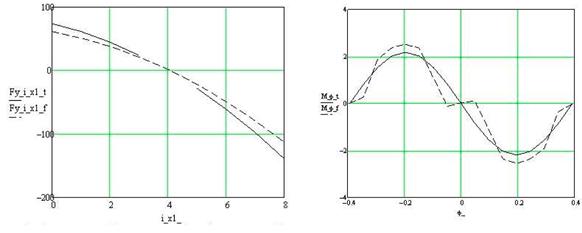
Из рис. 4 (б - в) видно, что, результаты моделирования различными иетодами качественно совпадают. Завышенные результаты силы в аналитической модели объясняются пренебрежением индуктивностями рассеяния.

Из рис. 4 (г) видно, что полученные моменты также практически полностью совпадают.

Данная модель позволяет получить зависимости радиальных сил и момента от токов в обмотках и положения ротора. Вычисляя командные силы в зависимости от положения ротора (например по закону ПИД – регулирования) и зная зависимости сил от токов, можно рассчитать командные токи средствами вычислительной техники (в качестве вычислительного устройства может служить контроллер). В усилителях мощности формируются токи, необходимые для удержания ротора в центральном положении.