Управляющие элементы интерфейса и область ввода исходных

Данных; 2 – область задания и отображения найденных

Коэффициентов автопилота; 3 – область отображения графической информации данных переходного процесса; 4.1,4.2 – области

Построения ЛАФЧХ контура управления

Таким образом, применение данного ПО позволяет сократить время проектирования САУ и подобрать значения коэффициентов автопилота.

Список литературы

1. Распопов В.Я., Товкач С.Е. Авионика малоразмерных беспилотных летательных аппаратов // Мир авионики, 2009 г, №3. – С. 39 - 47.

2. Расчетный и лабораторный практикум по микросистемной авионике: учебное пособие для вузов/под ред. проф., д-ра техн. наук В.Я. Распопова. Тула: Изд-во ТулГУ, 2011. 211 с.

СИНХРОНИЗАЦИЯ ДВИЖЕНИЯ РАБОЧИХ МАШИН С ПОМОЩЬЮ ЦЕПНОГО КОНВЕЙЕРА

Устранение существенного недостатка применяемых в настоящее время схем электромеханического привода автоматических роторных линий, заключающегося в существовании жесткой кинематической связи рабочих роторов, на основе цепного дифференциального конвейера с несколькими степенями свободы и индивидуальных приводов рабочих машин, синхронное движение которых осуществляется с помощью системы автоматического управления, является наиболее универсальным [1]. Однако в некоторых случаях (в линиях малой протяженности, при использовании рабочих машин с малыми нагрузками) может оказаться экономически нецелесообразным. Более простым решением в этом случае является использование цепного дифференциального конвейера с синхронизацией движения рабочих машин за счет сил натяжения в ветвях этого конвейера. На рис. 1 приведен простейший вариант предлагаемого решения для линии, состоящей из двух рабочих машин.

Цепной дифференциальный конвейер 4 охватывает рабочие машины 3, 12, две вспомогательные звездочки с неподвижными осями вращения 6, 11 и две звездочки с подвижными осями вращения 7, 10, подпружиненные пружинами 5, 9 относительно станины 8. Привод линии имеет два электродвигателя 1, 14 и два дифференциальных редуктора (ДР) 2, 13 с двумя степенями свободы каждый. Первый вход каждого редуктора соединен с соответствующим двигателем, выходы редукторов связаны с рабочими машинами. Вторые входы редукторов связаны между собой уравнительной реактивной связью 15, предназначенной для выравнивания нагрузок на выходах редукторов. Рассматриваемая механическая система будет иметь две степени свободы, что позволяет рабочим машинам двигаться независимо друг от друга и обеспечивает развязку движения рабочих машин при аварийной остановке одного из роторов. При нормальном функционировании линии появляющееся рассогласование рабочих машин приводит к перераспределению сил натяжения в цепи, что, в свою очередь, вызывает изменение угловых скоростей роторов и устранение этого рассогласования. Таким образом, обеспечивается необходимое согласование рабочего и транспортного движений.

Увеличение нагрузок на цепной конвейер может привести к его преждевременному выходу из строя. Поэтому при проектировании привода необходимо иметь возможность рассчитывать силы натяжения ветвей цепи в различных режимах движения. Ниже рассматривается решение этой задачи в основном - рабочем (установившемся) режиме движения линии.

Для получения зависимости между моментами на входе и выходе дифференциальных редукторов рассмотрим статику привода линии (рис. 2). Примем, что в приводе используются одинаковые редукторы. Тогда кинематика дифференциальных редукторов будет описываться системой уравнений

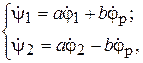
где 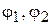– углы поворота входных звеньев редуктора; 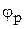– угол поворота реактивной связи; 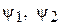– углы поворота выходных звеньев редукторов и связанных с ними рабочих машин; 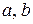– передаточные отношения дифференциальных редукторов.

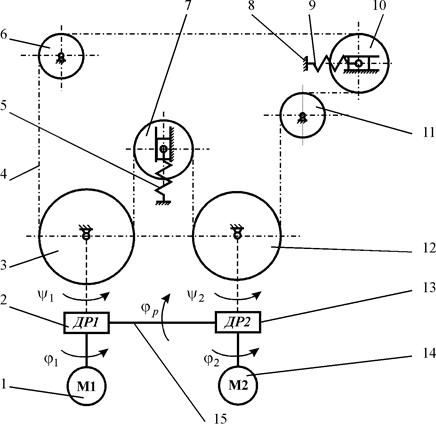
Рис. 1. Структурная схема привода с синхронизацией движения
роторов с помощью цепного дифференциального конвейера

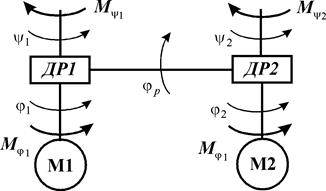
Рис. 2. Расчетная схема системы дифференциальных редукторов

Обозначая моменты, развиваемые двигателями 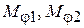, а моменты, приложенные к выходам редукторов со стороны рабочих машин - 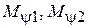, и применяя принцип возможных перемещений, получим, что распределение моментов на выходах редукторов при одном и двух включенных двигателях одинаково

Расчетная схема цепного дифференциального конвейера приведена на рис. 3. Неподвижные звездочки не оказывают влияния на распределение сил в ветвях конвейера и введены для получения его необходимой конфигурации. Для выявления влияния только особенностей рассматриваемой схемы на перераспределение сил в ветвях конвейера в первом приближении будем считать цепь абсолютно гибкой упругой нитью, звездочки заменим круглыми шкивами и примем, что форма ветвей гибкого звена на участках между шкивами прямолинейна [2].

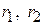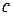Введем обозначения: – радиусы роторов; – радиусы подвижных звездочек; – коэффициент упругости гибкого звена;
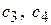– коэффициенты упругости пружин, связывающих оси подвижных звездочек со станиной; 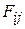– натяжения в ветвях гибкой связи, причем 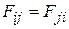; 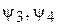– углы поворота подвижных звездочек.

Поступательное перемещение осей подвижных звездочек определим координатами 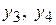, отсчитываемыми от положения статического равновесия звездочек в ненагруженном конвейере. Моменты, действующие на рабочих машинах, представим в виде

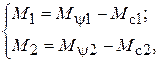
где 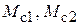– моменты сил технологического сопротивления.

Для определения деформаций упругих звеньев и сил упругости в них (при отсутствии внешних нагрузок) воспользуемся условием [3]

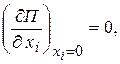(1)

где 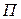– потенциальная энергия системы; 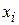– обобщенные координаты, в качестве которых примем .

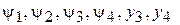Преобразуя (1), будем иметь

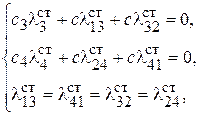
где 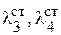– деформации пружин подвижных звездочек в положении статического равновесия; 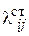– деформации ветвей гибкой связи в положении статического равновесия.

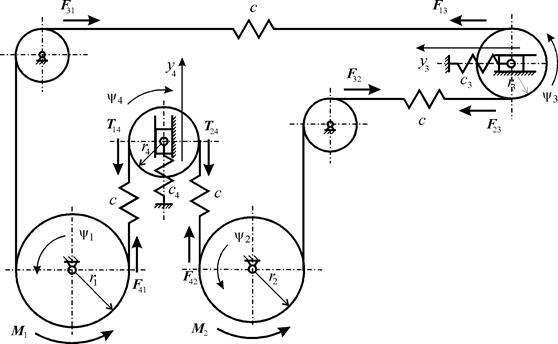
Рис. 3. Расчетная схема цепного дифференциального конвейера

Отсюда видно, что силы натяжения во всех ветвях гибкой связи одинаковы. Обозначая эти силы 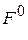, получим значения сил упругости пружин ненагруженного конвейера в виде:

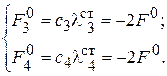
Для определения перемещений элементов системы и величин сил упругости при нагружении рабочих машин моментами воспользуемся уравнениями [3]:

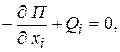(2)

где 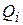– обобщенные силы.

В рассматриваемой системе обобщенные силы будут действовать только по координатам 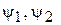, 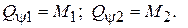Остальные обобщенные силы равны нулю: .

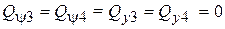В режиме установившегося движения

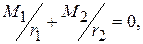(3)

что является необходимым условием нахождения цепного конвейера в равновесии.

При выполнении условия (3), система уравнений (2) будет линейно зависимой, т.е. формально может иметь бесконечное множество решений. Для получения одного решения задаем значение одной из координат, например, 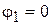, что равносильно заданию начала отсчета угловых координат.

Решая систему (2) относительно обобщенных координат и представляя силы натяжения в ветвях гибкой связи в ви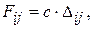де где
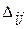– деформации ветвей гибкой связи, которые можно выразить через обобщенные координаты системы

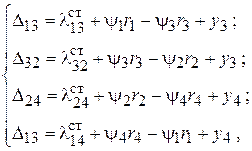
получим зависимости для определения сил натяжения в ветвях конвейера

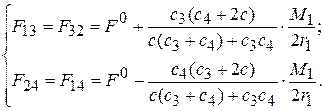
Для анализа влияния моментов, приложенных к роторам, на перераспределение сил в системе представим силы натяжения цепи следующим образом

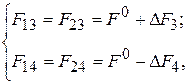
где

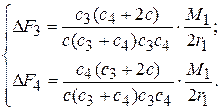
Переходя к безразмерным величинам, получим

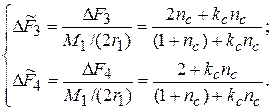(4)

Здесь 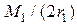– приращение силы натяжения в ведущей ветви недеформируемого конвейера, вызываемое действием крутящего момента ; .

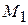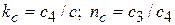Графики зависимостей 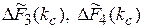при различных значениях параметра 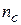приведены на рис. 4. Анализ зависимостей (4) и приведенных графиков позволяет сделать следующие выводы:

1. При работе линии под нагрузкой силы натяжения в ветвях цепного конвейера зависят от жесткости цепи и пружин.

2. Для любых коэффициентов упругости пружин .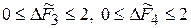

3. Если коэффициенты упругости пружин имеют одинаковый порядок 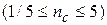, то .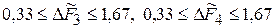

4. При увеличении параметра 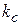, что соответствует увеличению жесткости пружин по сравнению с жесткостью цепи, ;

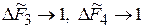5. При одинаковых пружинах 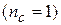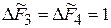и не зависят от их коэффициентов упругости.

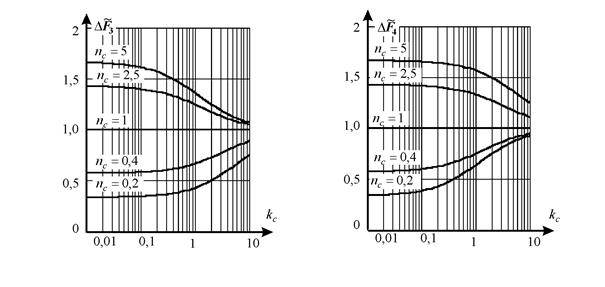
Рис. 4. Влияние упругих характеристик привода на распределение сил
в ветвях цепного конвейера

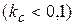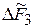6. Если жесткость пружин мала по сравнению с жесткостью цепи , то и 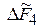практически не зависят от жесткости цепи и могут быть определены по приближенным формулам: .

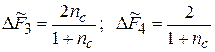Список литературы

1. Крюков В.А., Прейс В.В. Системы приводов рабочих движений автоматических роторных и роторно-конвейерных линий / Вестник машиностроения. 2003. № 1. С. 36-41.

2. Куровский Ф.М. Теория плоских механизмов с гибкими связями. М.: Машгиз, 1963. 204 с.

3. Добронравов В.В. Основы аналитической механики. М.: Высшая школа, 1976. 264 с.

<1 2 345 6 7 >

Дата добавления: 2020-10-14; просмотров: 308;