ОПТИМИЗАЦИЯ ДИНАМИЧЕСКИХ ПРОЦЕССОВ В ЦЕПНЫХ ТРАНСПОРТНЫХ КОНВЕЙЕРАХ АВТОМАТИЧЕСКИХ РОТОРНО-КОНВЕЙЕРНЫХ ЛИНИЙ
Переход от автоматических роторных к автоматическим роторно-конвейерным линиям (АРКЛ), способным обеспечить достижение более высокого уровня автоматизации и производительности, привел к появлению в линиях цепного транспортного конвейера. Характерной особенностью цепных передач, к которым относится и указанный конвейер, является непостоянство передаточного отношения, причиной чего служит хордальное расположение звеньев цепи на зубьях звездочки и рассогласование начала входа первого звена ветви цепи в зацепление с ведущей звездочкой и выхода последнего звена ветви из зацепления с ведомой звездочкой [1].
При использовании в качестве системы синхронизации движения роторов зубчатых передач эта особенность приводит к дополнительным нагрузкам на цепной конвейер и его быстрому выходу из строя. Если синхронизация движения осуществляется только с помощью цепного конвейера, то неравномерность движения будет накапливаться при переходе от ротора к ротору и, в конце концов, может достигнуть недопустимых значений. Переменное передаточное отношение также приводит к появлению дополнительных динамических нагрузок на элементы цепного конвейера, что снижает долговечность и надежность линии и отрицательно сказывается на качестве ее работы. Поэтому особую важность имеет определение неравномерности движения ведомых звеньев цепной передачи и разработка методов ее уменьшения.
Используемые в настоящее время методики исследования кинематики и проектирования цепных передач [2, 3, 4] ориентированы на цепные передачи общего машиностроения. Характерными особенностями таких передач являются большие межосевые расстояния [2] 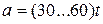 , где
, где
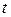 – шаг цепи и, соответственно, большое число звеньев цепи в ветвях передачи. При таких значениях геометрических параметров передачи ветви цепи практически не поворачиваются относительно первоначального положения, что позволяет считать их движение поступательным. Это значительно упрощает кинематический анализ передачи и в то же время позволяет получить результаты с приемлемой для практики точностью.
– шаг цепи и, соответственно, большое число звеньев цепи в ветвях передачи. При таких значениях геометрических параметров передачи ветви цепи практически не поворачиваются относительно первоначального положения, что позволяет считать их движение поступательным. Это значительно упрощает кинематический анализ передачи и в то же время позволяет получить результаты с приемлемой для практики точностью.
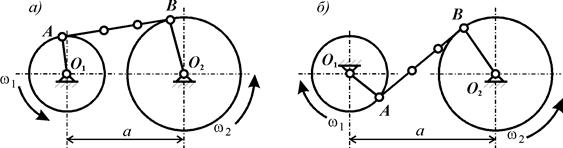
В цепных конвейерах АРКЛ, отличающихся малыми межосевыми расстояниями и малым числом звеньев в ветвях цепи (как правило, не более 4 – 5 звеньев), такой подход может привести не только к количественным погрешностям, но и качественно неверным результатам. Еще одной особенностью цепного конвейера АРКЛ является наличие многозвенных цепных контуров и расположение смежных звездочек снаружи цепного контура. Схему, соответствующую расположению звездочек внутри цепного контура (рис. 1, а), назовем сборкой 1, а схему, соответствующую расположению смежных звездочек снаружи цепного контура – сборкой 2 (рис. 1, б).


А б
Рис. 1. Расположение звездочек цепного конвейера:
а – сборка 1; б – сборка 2
Для получения передаточного отношения участка цепной передачи, состоящей из двух звездочек, ее можно рассматривать (в пределах поворота ведущей звездочки на один угловой шаг) как шарнирный четырехзвенник (рис. 2), в котором ведущая звездочка заменена кривошипом 1 радиусом 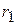 , ведомая – кривошипом 2 радиусом
, ведомая – кривошипом 2 радиусом 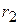 , а ведущая ветвь цепи – шатуном длиной
, а ведущая ветвь цепи – шатуном длиной 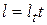 , причем число звеньев цепи
, причем число звеньев цепи 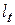 , содержащихся в рассматриваемой ветви AB обязательно должно быть целым [2]. Радиусы кривошипов являются радиусами делительных окружностей звездочек и рассчитываются по формулам
, содержащихся в рассматриваемой ветви AB обязательно должно быть целым [2]. Радиусы кривошипов являются радиусами делительных окружностей звездочек и рассчитываются по формулам
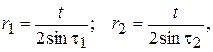
где 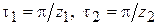 – половина углового шага звездочки 1 и 2, соответственно;
– половина углового шага звездочки 1 и 2, соответственно; 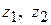 – числа зубьев звездочек.
– числа зубьев звездочек.
Кроме того, обозначим: 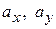 - проекции межосевого расстояния
- проекции межосевого расстояния 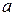 на оси координат
на оси координат 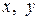 (см. рис. 2);
(см. рис. 2); 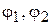 - углы поворота кривошипов
- углы поворота кривошипов 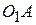 и
и 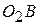 , проведенных из центров вращения звездочек в центры шарниров цепи, находящихся в зацеплении с ведущей и ведомой звездочками;
, проведенных из центров вращения звездочек в центры шарниров цепи, находящихся в зацеплении с ведущей и ведомой звездочками; 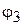 - угол поворота шатуна
- угол поворота шатуна 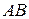 .
.
В общем случае при 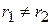 вход и выход шарниров цепи в зацепление с зубьями ведущей и ведомой звездочек будет происходить не одновременно. Так для схемы, показанной на рис. 2, ведущая ветвь цепи будет последовательно занимать положения
вход и выход шарниров цепи в зацепление с зубьями ведущей и ведомой звездочек будет происходить не одновременно. Так для схемы, показанной на рис. 2, ведущая ветвь цепи будет последовательно занимать положения 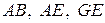 . Это приводит к тому, что число звеньев ветви цепи будет меняться во время движения и, следовательно, являться некоторой неизвестной пока функцией от угла поворота ведущей звездочки.
. Это приводит к тому, что число звеньев ветви цепи будет меняться во время движения и, следовательно, являться некоторой неизвестной пока функцией от угла поворота ведущей звездочки.
Для получения функции положения заменяющего шарнирного четырехзвенника 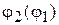 запишем уравнение замкнутого векторного контура
запишем уравнение замкнутого векторного контура 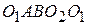 (см. рис. 2)
(см. рис. 2)
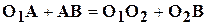
и спроецируем его на оси координат 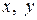
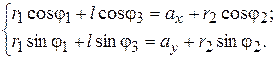 (1)
(1)
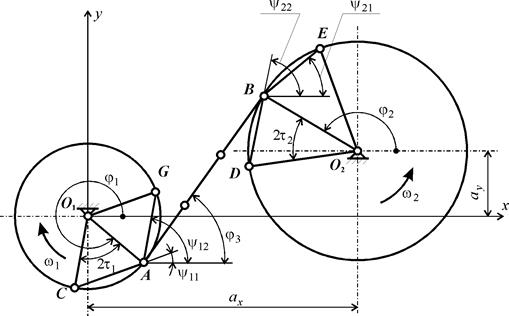
Рис. 2. Определение передаточного отношения цепной передачи
Из рис. 2 видно, что условие зацепления цепи со звездочкой 1 в шарнире 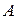 будет иметь вид
будет иметь вид
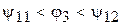 , (2)
, (2)
а условие зацепления цепи со звездочкой 2 в шарнире 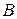
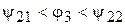 . (3)
. (3)
Выражая из треугольников 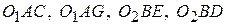 вспомогательные углы
вспомогательные углы 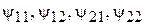 через углы поворота звездочек и их угловые шаги и подставляя найденные зависимости в (2), (3), получим
через углы поворота звездочек и их угловые шаги и подставляя найденные зависимости в (2), (3), получим
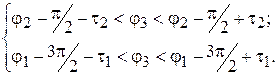 (4)
(4)
Система уравнений и неравенств (1), (4), дополненная уравнением, связывающим неизвестное число звеньев в ветви цепи с ее длиной
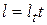 , (5)
, (5)
позволяет определить функцию положения шарнирного четырехзвенника, а, следовательно, и цепной передачи. Указанная система является нелинейной и, кроме того, содержит целочисленную переменную 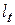 . Поэтому ее решение может быть выполнено только численными методами.
. Поэтому ее решение может быть выполнено только численными методами.
Угол поворота звездочки 1 в системе уравнений (1) изменяется в пределах 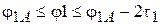 . В момент входа шарнира
. В момент входа шарнира 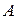 в зацепление, определяемый углом
в зацепление, определяемый углом 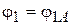 , хорда
, хорда 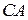 и ветвь
и ветвь 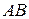 должны располагаться на одной прямой, т.е.
должны располагаться на одной прямой, т.е.
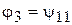 . (6)
. (6)
Аналогично, пересопряжение цепи на звездочке 2, будет определяться углом 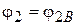 , удовлетворяющим условию
, удовлетворяющим условию
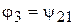 . (7)
. (7)
Решая системы уравнений и неравенств (1), (3), (5), (6) и (1), (2), (5), (7), можно определить значения углов 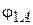 и
и 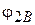 , соответственно.
, соответственно.
Дифференцируя уравнения (1) по времени и выполняя необходимые преобразования, найдем передаточные отношения (первые передаточные функции) рассматриваемой системы
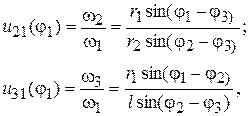
а затем угловые скорости звездочки 2 и ветви цепи
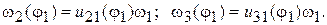
Коэффициент неравномерности угловой скорости звездочки 2
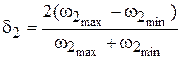
или
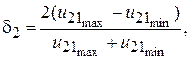
где 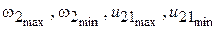 – максимальное и минимальное значения угловой скорости звездочки и передаточного отношения, соответственно.
– максимальное и минимальное значения угловой скорости звездочки и передаточного отношения, соответственно.
Анализ кинематики цепного контура с двумя звездочками на основе полученных аналитических зависимостей выполнялся численными методами с помощью пакета программ MathСad. Результаты этого анализа представлены на рис. 3-5.
График на рис. 3 иллюстрирует типичную зависимость передаточного отношения 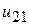 (а, следовательно, и угловой скорости ведомой звездочки
(а, следовательно, и угловой скорости ведомой звездочки 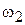 ) от угла поворота ведущей звездочки
) от угла поворота ведущей звездочки 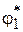 в пределах ее поворота на один угловой шаг. Как видно из рисунка, колебания передаточного отношения составляют примерно 8 % от его среднего значения, причем в отличие от известных графиков [3], построенных на основе приближенных зависимостей, он несимметричен относительно середины углового шага, а пересопряжения зацепления на звездочках приводят к изменению числа звеньев в ветви цепи.
в пределах ее поворота на один угловой шаг. Как видно из рисунка, колебания передаточного отношения составляют примерно 8 % от его среднего значения, причем в отличие от известных графиков [3], построенных на основе приближенных зависимостей, он несимметричен относительно середины углового шага, а пересопряжения зацепления на звездочках приводят к изменению числа звеньев в ветви цепи.
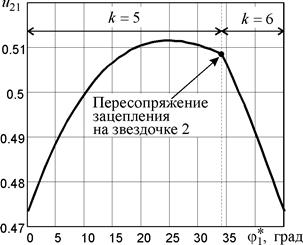
Рис. 3. Зависимость передаточного отношения цепной передачи
от угла поворота ведущей звездочки
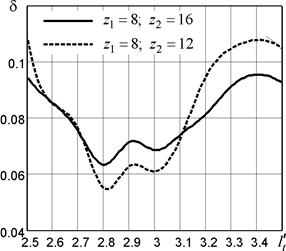
Рис. 4. Зависимость коэффициента неравномерности движения от 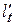
Согласно выполненным ранее исследованиям [2] наименьшее значение коэффициента неравномерности, обеспечивающее оптимальное протекание динамических процессов в передаче, соответствует так называемому синфазному движению звездочек, при котором общая касательная, проведенная к делительным окружностям смежных звездочек 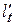 , кратна шагу цепи. Исследование зависимости коэффициента неравномерности движения ведомой звездочки
, кратна шагу цепи. Исследование зависимости коэффициента неравномерности движения ведомой звездочки 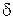 от
от 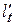 , выполненное на основе уточненных зависимостей (см. рис. 4), показало, что при малых межосевых расстояниях передачи с синфазным движением звездочек не являются оптимальными. Так, для рассмотренных примеров наименьшее значение коэффициента неравномерности обеспечивается при
, выполненное на основе уточненных зависимостей (см. рис. 4), показало, что при малых межосевых расстояниях передачи с синфазным движением звездочек не являются оптимальными. Так, для рассмотренных примеров наименьшее значение коэффициента неравномерности обеспечивается при 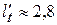 , причем разность между наименьшим значением коэффициента неравномерности и значением этого коэффициента для синфазной передачи (
, причем разность между наименьшим значением коэффициента неравномерности и значением этого коэффициента для синфазной передачи ( 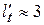 ) достигает 15 %.
) достигает 15 %.
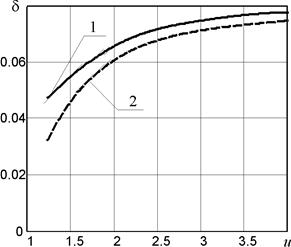
Рис. 5. Зависимость минимально возможного коэффициента
неравномерности движения от передаточного отношения
Анализ зависимости коэффициента неравномерности 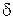 от передаточного числа передачи
от передаточного числа передачи 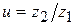 при постоянных числе зубьев меньшей звездочки
при постоянных числе зубьев меньшей звездочки 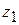 и межосевом расстоянии
и межосевом расстоянии 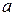 (см. рис. 5) показал, что увеличение передаточного числа приводит к увеличению минимально возможного значения коэффициента неравномерности (кривая 2). Эта тенденция справедлива и для синфазной передачи (кривая 1) [2]. Однако в области малых передаточных чисел
(см. рис. 5) показал, что увеличение передаточного числа приводит к увеличению минимально возможного значения коэффициента неравномерности (кривая 2). Эта тенденция справедлива и для синфазной передачи (кривая 1) [2]. Однако в области малых передаточных чисел 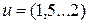 выбор значения
выбор значения 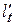 (а, следовательно, и межосевого расстояния) на основе уточненных зависимостей позволяет существенно уменьшить коэффициент неравномерности движения.
(а, следовательно, и межосевого расстояния) на основе уточненных зависимостей позволяет существенно уменьшить коэффициент неравномерности движения.
Список литературы
1. Машиностроение. Энциклопедия / Ред. совет: К.В. Фролов (пред.) и др. М.: Машиностроение. Детали машин. Конструкционная прочность. Трение, износ, смазка. Т. IV-1 / Д.Н. Решетов, А.П. Гусенков, Ю.Н. Дроздов и др.; Под общ. ред. Д.Н. Решетова. 1995. 864 с.
2. Готовцев А.А., Котенок И.П. Проектирование цепных передач. М.: Машиностроение, 1982. 336 с.
3. Воробьев Н.В. Цепные передачи. М.: Машиностроение, 1968. 252 с.
4. Глущенко И.П., Петрик А.А. Цепные передачи. Киев: Техника, 1973. 104 с.
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОДНОКАНАЛЬНОГО ВИБРАЦИОННОГО ЗАГРУЗОЧНОГО УСТРОЙСТВА С АСИНХРОННЫМ ВОЗБУЖДЕНИЕМ КОЛЕБАНИй
Применение вибрационных загрузочных устройств (ВЗУ) с электромагнитным приводом и раздельным возбуждением колебания в горизонтальном и вертикальном направлениях позволило повысить относительную скорость виброперемещения дискретных предметов обработки в безотрывном режиме на порядок, т. е. до 400 мм/с.
Однако, это достижение повлекло за собой ряд усложнений их конструкций: возросла энергоемкость; металлоемкость; усложнилась схема управления электромагнитными приводами она стала двухканальной. Поэтому возникла задача упростить конструкцию - реализовать одноканальную схему управления только лишь привода горизонтальных колебаний, а вертикальные колебания возбуждать механической частью привода путем отбора мощности у привода горизонтальных колебаний.
На рис. 1 представлена упругая система, единая для горизонтального и вертикального приводов, состоящая из крестообразно расположенных витых цилиндрических пружин 1-8. Пружины 2, 3, 5, 7 - основные пружины для горизонтального привода и их жесткости равны
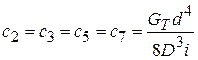 ,
,
где 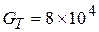 МПа – модуль упругости;
МПа – модуль упругости; 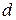 – диаметр проволоки, мм;
– диаметр проволоки, мм;
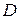 – средний диаметр пружины, мм; i – число рабочих витков.
– средний диаметр пружины, мм; i – число рабочих витков.
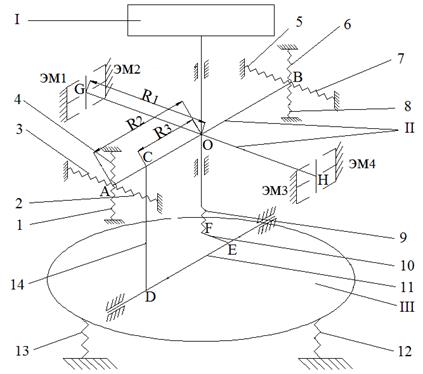
Рис. 1. Общая структурная схема вибропривода:
1-8 – витые цилиндрические пружины; 9 – центральная пружина;
Дата добавления: 2020-10-14; просмотров: 665;











