Механические колебания и волны

31. Кинематическое уравнение гармонических колебаний материальной точки:

,

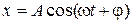где x – смещение; A – амплитуда колебаний; w – круговая или циклическая частота; j – начальная фаза.

32. Скорость материальной точки, совершающей гармонические колебания:

.

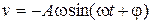33. Ускорение материальной точки, совершающей гармонические колебания:

.

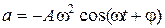34. Сложение гармонических колебаний одного направления и одинаковой частоты:

а) амплитуда результирующего колебания

;

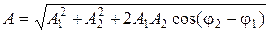б) начальная фаза результирующего колебания

.

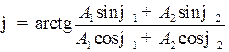35. Траектория точки, участвующей в двух взаимно перпендикулярных колебаниях ( ):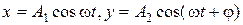

а) 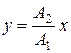(если разность фаз );

б) 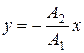(если разность фаз );

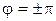в) 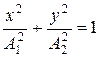(если разность фаз ).

36. Уравнение плоской бегущей волны:

,

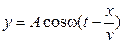где y – смещение любой из точек среды с координатой x в момент времени t; n – скорость распространения колебаний в среде.

37. Связь разности фаз ∆j колебаний с расстоянием ∆x между точками среды, отсчитанным в направлении распространения колебаний:

,

где l – длина волны.

ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ

Основные формулы