Динамика материальной точки и твердого тела

ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ

Основные формулы

Кинематика материальной точки и твердого тела

1. Кинематическое уравнение движения материальной точки (центра масс твердого тела) вдоль оси x:

x = f (t),

где f (t) – некоторая функция времени.

2. Средняя скорость:

.

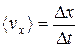3. Средняя путевая скорость:

,

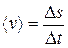где Ds – путь, пройденный точкой за интервал Dt. Путь Ds в отличие от разности координат ( 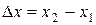) не может убывать и принимать отрицательные значения, т.е. . Поэтому .

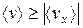4. Мгновенная скорость:

.

5. Среднее ускорение:

.

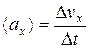6. Мгновенное ускорение:

.

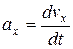7. Кинематическое уравнение движения материальной точки по окружности:

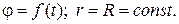
8. Угловая скорость:

.

9. Угловое ускорение:

.

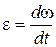10. Связь между линейными и угловыми величинами, характеризующими движение точки по окружности:

,

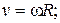
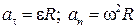где n – линейная скорость; a_t и a_n – тангенциальное и нормальное ускорение; w – угловая скорость; e – угловое ускорение; R – радиус окружности.

11. Полное ускорение:

или .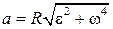

12. Угол между полным ускорением 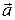и нормальным :

.

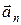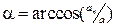Динамика материальной точки и твердого тела

13. Импульс материальной точки m, движущейся поступательно со скоростью v:

.

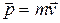14. Второй закон Ньютона:

где 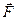– сила, действующая на тело.

15. Основное уравнение динамики вращательного движения относительно неподвижной оси:

,

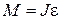где M – результирующий момент внешних сил, действующих на тело; e – угловое ускорение; 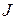– момент инерции тела относительно оси вращения.

16. Моменты инерции некоторых тел массы m относительно оси, проходящей через центр масс:

а) стержня длины 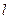относительно оси, перпендикулярной стержню и проходящей через центр масс,

;

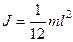б) обруча (тонкостенного цилиндра) относительно оси, перпендикулярной плоскости обруча (совпадающей с осью цилиндра),

,

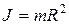где R – радиус обруча (цилиндра);

в) диска радиусом R относительно оси, перпендикулярной плоскости диска,

.

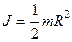17. Момент импульса тела, вращающегося относительно неподвижной оси:

,

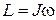где w – угловая скорость тела.

18. Силы, рассматриваемые в механике:

а) сила упругости

,

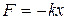где k – коэффициент упругости (в случае пружины – жесткость); x – абсолютная деформация;

или s = –Еe,

где s – упругое напряжение, Е – модуль Юнга, e – относительная деформация;

б) сила тяжести

;

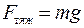в) сила гравитационного взаимодействия

,

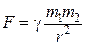где g – гравитационная постоянная; m₁ и m₂ – массы взаимодействующих тел; r – расстояние между телами (тела рассматриваются как материальные точки). В случае гравитационного взаимодействия силу можно выразить также через напряженность G гравитационного поля:

;

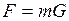г) сила трения (скольжения)

,

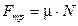где m – коэффициент трения; N – сила нормального давления.