Работа и механическая энергия

19. Закон сохранения импульса:

,

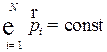или для двух тел (i = 2):

,

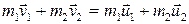где 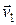и – скорости тел в момент времени, принятый за начальный; и 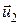скорости тех же тел в момент времени, принятый за конечный.

20. Кинетическая энергия тела, движущегося поступательно:

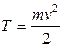или .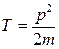

21. Потенциальная энергия:

а) упругодеформированной пружины

П = ,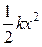

где k – жесткость пружины; x – абсолютная деформация;

б) гравитационного взаимодействия

П = ,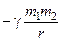

где g – гравитационная постоянная; m₁ и m₂ – массы взаимодействующих тел; r – расстояние между ними (тела рассматриваются как материальные точки);

в) тела в однородном поле силы тяжести

П = ,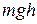

где g – ускорение свободного падения; h – высота тела над уровнем, принятым за нулевой (формула справедлива при условии h << R, где
R – радиус Земли).

22. Закон сохранения механической энергии:

E = T + П = const.

23. Работа A, совершаемая внешними силами, определяется как мера изменения энергии системы:

.

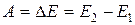24. Закон сохранения момента импульса системы тел, вращающихся вокруг неподвижной оси:

,

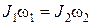где и w₁ – момент инерции системы тел и угловая скорость вращения в момент времени, принятый за начальный; 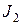и w₂ – момент инерции и угловая скорость в момент времени, принятый за конечный.

25. Кинетическая энергия тела, вращающегося вокруг неподвижной оси:

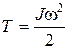или .

Механика жидкостей

26. Гидростатическое давление столба жидкости на глубине h:

,

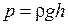где r – плотность жидкости.

27. Уравнение Бернулли для стационарного течения идеальной несжимаемой жидкости:

,

где p – статическое давление жидкости для определенного сечения трубки тока; v – скорость жидкости для этого же сечения; rv²/2 – динамическое давление жидкости для этого же сечения; h – высота, на которой расположено сечение; rgh – гидростатическое давление.

28. Формула Пуазейля, позволяющая определить объем жидкости, протекающей за время t через капиллярную трубку длиной l:

,

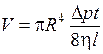где R – радиус трубки; ∆p – разность давлений на концах трубки;
h – динамическая вязкость жидкости.

29. Число Рейнольдса, определяющее характер движения жидкости:

,

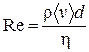где r – плотность жидкости; <v> – средняя по сечению трубки скорость жидкости; d – характерный линейный размер, например, диаметр трубы.

30. Формула Стокса, позволяющая определить силу сопротивления, действующую на медленно движущийся в вязкой среде шарик:

,

где r – радиус шарика; v – его скорость.