Основные положения молекулярно-кинетической теории газов

1. Количество вещества однородного газа (в молях):

n = 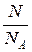или n = ,

где N – число молекул газа; N_A – число Авогадро; m – масса газа; m – молярная масса газа.

Если система представляет смесь нескольких газов, то количество вещества системы равно:

n = n₁+n₂+...+n_n =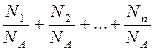

или

n = ,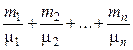

где n_i, N_i, m_i, m_i – соответственно количество вещества, число молекул, масса, молярная масса i-й компоненты смеси.

2. Уравнение Менделеева-Клапейрона (уравнение состояния идеального газа):

,

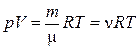где m – масса газа; m – молярная масса газа; R – универсальная газовая постоянная; n= m/m – количество вещества; T – термодинамическая температура Кельвина.

3. Опытные газовые законы, являющиеся частными случаями уравнения Менделеева-Клапейрона для изопроцессов:

а) закон Бойля-Мариотта (изотермический процесс: T = const;
m = const):

pV = const

или для двух состояний газа:

p₁V₁ = p₂V₂,

где p₁ и V₁ – давление и объем газа в начальном состоянии; p₂ и V₂ – те же величины в конечном состоянии;

б) закон Шарля (изобарический процесс: p = const, m = const):

или для двух состояний:

где V₁ и T₁ – объем и температура газа в начальном состоянии; V₂ и T₂ – те же величины в конечном состоянии;

в) закон Гей-Люссака (изохорический процесс – V = const,
m = const):

или для двух состояний:

где p₁ и T₁ – давление и температура газа в начальном состоянии; p₂ и T₂ – те же величины в конечном состоянии;

г) объединенный газовый закон (m = const):

или для двух состояний:

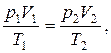
где p₁, V₁, T₁ – давление, объем и температура газа в начальном состоянии; p₂, V₂, T₂ – те же величины в конечном состоянии.

4. Закон Дальтона, определяющий давление смеси газов:

p = p₁ + p₂ +...+ p_n,

где p_i – парциальные давления компонентов смеси; n – число компонентов смеси.

5. Молярная масса смеси газов:

где m_i – масса i-го компонента смеси; n_i = m_i/m_i – количество вещества i-го компонента смеси; n – число компонентов смеси.

6. Массовая доля w_i i-го компонента смеси газа (в долях единицы или процентах):

,

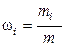где m – масса смеси.

7. Концентрация молекул (число молекул в единице объема):

,

где N – число молекул, содержащихся в данной системе; r – плотность вещества. Формула справедлива не только для газов, но и для любого агрегатного состояния вещества.

8. Основное уравнение молекулярно-кинетической теории газов:

náЕ_постñ,

где áЕ_постñ – средняя кинетическая энергия поступательного движения молекулы.

9. Средняя кинетическая энергия поступательного движения молекулы:

áЕ_постñ = kT,

где k – постоянная Больцмана.

10. Средняя полная кинетическая энергия молекулы:

áЕñ = kT,

где i – число степеней свободы молекулы.

11. Зависимость давления газа от концентрации молекул и температуры:

p = nkT.

12. Скорости молекул:

средняя квадратичная ;

средняя арифметическая ;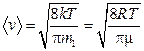

наиболее вероятная ,

где m₁ – масса одной молекулы.

13. Относительная скорость молекулы:

где v – скорость данной молекулы.

14. Распределение скоростей молекул по Максвеллу:

где DN(v) – число молекул, скорости которых лежат в интервале от v до v + Dv.

15. Барометрическая формула:

или

,

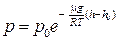где р и р₀ – давление газа на высоте h и h₀.

16. Распределение Больцмана:

,

где n₀ и Е₀ – концентрация и потенциальная энергия частиц на высоте h₀.

17. Средняя длина свободного пробега молекул:

,

где <v> – средняя арифметическая скорость, <z> – среднее число столкновений каждой молекулы с остальными в единицу времени, s – эффективный диаметр молекулы, n – число молекул в единице объема (концентрация молекул). Общее число столкновений всех молекул в единице объема за единицу времени Z = <z> n/2.

18. Масса, перенесенная за время Dt при диффузии (закон Фика):

,

где Dr/Dх – градиент плотности в направлении, перпендикулярном к площадке DS, D = <v><l>/3 – коэффициент диффузии (<v> – средняя арифметическая скорость, <l> – средняя длина свободного пробега молекул).

19. Импульс, перенесенный газом за время Dt, определяет силу внутреннего трения F_тр в газе (закон Ньютона):

,

где Dv/Dx – градиент скорости течения газа в направлении, перпендикулярном к площадке DS, h = <v><l>r/3 – динамическая вязкость.

20. Количество теплоты, перенесенное за время Dt вследствие теплопроводности, определяется формулой (закон Фурье):

,

где DТ/Dx – градиент температуры в направлении, перпендикулярном к площадке DS, К = <v><l>с_Vr/3 – коэффициент теплопроводности.